数据结构与算法基础
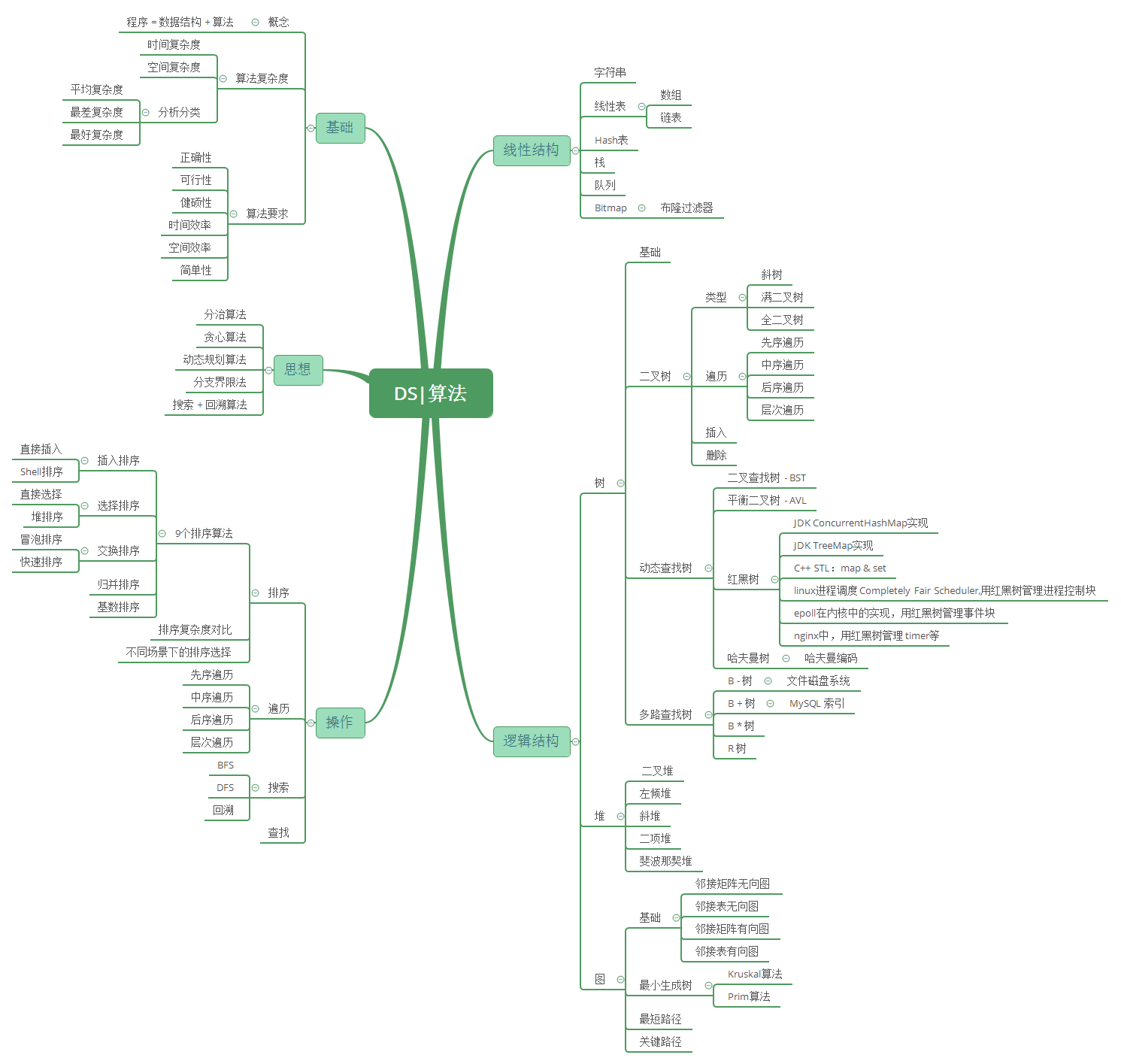
先主干再细节,细枝末节的内容是海量的!如果你不是出书或者授课,真的没必要把所有概念都梳理完整。
亲生经历,整理知识结构体系真的非常耗费时间和精力!大脑不停地在做复制粘贴的重复工作,空荡荡的,简直快要吐了!高考都在不停地整理各大学科的知识结构体系,而缺乏做题练习的实战经验,最后考得很不理想。那几本幸幸苦苦耗时两年整理的学科知识体系,考试结束后就当废品卖掉了!其实,那时候,书店早就有各学科知识体系手册了,并且都很完善,自己再花费大量时间精力总结几乎就是个错误的方法,但却没有任何人劝诫我,告诉我方法不对!最痛心不是这几本知识总结,也不是大量的时间和精力,而是这些高昂的付出成本,最后换来的结果!且不说还有其他心理压力等因素。工作几年后才知道大学是多么的关键,以至于每年高考那两天晚上都会做考试的噩梦!
知识结构体系这么耗费时间精力,那干脆直接用资料书籍上面结构体系,或者直接把别人整理的照搬整理进自己的体系。书籍上的知识结构是死的!知识是不断在推陈出新的,并且随时都需要加入自己的理解,纸质书籍和 PDF 非常的不灵活!真正对你最有效的是电子版可修改的文档,但很抱歉,书籍作者不会提供,他们要靠纸质版书籍赚稿费;博客、公众号作者几乎也不会提供,他们怕你拿完资料就走人,甚至怕你抄袭。表面上这些博主都在做帮助他人梳理技术知识,其实只不过是为自己博取名气罢了!真正有用的一手资料肯定不会白给你,要么收费,要么各种进群套路!真正让你看到的,基本上是一两年前的旧资料教程了,或者是一些零零散散的边角料!
怎样有效地构建自己的知识结构体系?
- 知识结构的主干框架一定要尽可能地保证准确,跟建高楼大厦一个道理,地基和骨架一定要确定无误;
- 主干框架不可能刚开始就能做到 100% 的完善,细节内容更是做不到完美,不断更新完善就好了;
- 用进废退,一切在于练习实践!知识体系整理得再完善,如果仅仅用来应付考试、面试,工作几乎不用,过个十天半月,就忘掉了。重复记忆可以保持,但工作就是用不到,不断花时间记忆不累吗?
- 兴趣成果驱动,理论概念驱不动,前提饭碗得保住。天天到处复制粘贴博客文章,大脑身心俱疲!整理完知识体系就扔一旁,继续整理其他知识体系,无尽地循环啊!全是大篇大篇的理论概念,很烦很累!一旦复制的细节内容过多,一天很快就这样占用了!日复一日、周复一周、月复一月、年复一年,好几年的年轻宝贵时光就这样耗费掉了。难道中年危机之前还在整理知识结构体系吗?等整理完整了,真正留给你工作实践的时间和机会还有多少啊?别再被那些各种超全的知识结构体系PUA了,超全完善的结构体系,他们是一个人整理出来的吗?他们是不用工作专门整理知识体系的吗?你真要照着他们一个团队的知识体系准备求职?赶紧挑重点实战练习,加深理解,理论概念用自己的理解描述,没工作,生活各种开销,最长三个月,超过这个期限,很容易被日常生活、孤独、无人理解等各种烦恼拖垮!真的,知识体系最佳的整理时间就是工作之余,没工作专门花时间整理,还专门挑那种超全完整的整理,那是别人花了大量工作之余时间整理的,足够耗费你半年一载!谁这么做啊?投入的时间成本巨大,最后换来的回报还是未知数,中间的过程还异常的艰苦无人理解!这个方法是那种破釜沉舟、拼死一搏、绝路逢生的策略,实属下下策!
- 知识体系内容元素多样化。一大堆长篇大段的理论概念,看一眼就足以让人犯困,这个快速信息时代,内容也要跟着调整,减少文字描述,加入图片和视频元素,更容易激起阅读欲望;
数据结构
概述
数据结构的存储方式
数据结构的存储方式只有两种:数组(顺序存储)和链表(链式存储)。
数据结构的基本操作
对于任何数据结构,其基本操作无非是遍历 + 访问,再具体一点就是:CRUD 增查改删。
数据结构种类很多,但它们存在的目的都是在不同的应用场景,尽可能高效地增删查改。
各种数据结构的遍历 + 访问无非两种形式:线性的和非线性的。
线性就是 for/while 迭代为代表,非线性就是递归为代表。
数组遍历框架,典型的线性迭代结构:
void traverse(int[] arr) {
for (int i = 0; i < arr.length; i++) {
// 迭代访问 arr[i]
}
}链表遍历框架,兼具迭代和递归结构:
/* 基本的单链表节点 */
class ListNode {
int val;
ListNode next;
}
void traverse(ListNode head) {
for (ListNode p = head; p != null; p = p.next) {
// 迭代访问 p.val
}
}
void traverse(ListNode head) {
// 递归访问 head.val
traverse(head.next);
}二叉树遍历框架,典型的非线性递归遍历结构:
/* 基本的二叉树节点 */
class TreeNode {
int val;
TreeNode left, right;
}
void traverse(TreeNode root) {
traverse(root.left);
traverse(root.right);
}你看二叉树的递归遍历方式和链表的递归遍历方式,相似不?再看看二叉树结构和单链表结构,相似不?如果再多几条叉,N 叉树你会不会遍历?
二叉树框架可以扩展为 N 叉树的遍历框架:
/* 基本的 N 叉树节点 */
class TreeNode {
int val;
TreeNode[] children;
}
void traverse(TreeNode root) {
for (TreeNode child : root.children)
traverse(child);
}N 叉树的遍历又可以扩展为图的遍历,因为图就是好几 N 叉棵树的结合体。图会出现环,可以用布尔数组 visited 做标记。
算法刷题策略参考
以商“成本-回报”的思维做算法题
自己是否可以搞定?自己搞不定需要什么样的外援?
从利益角度出发,肯定是希望自己能搞定,搞不定再请一个成本较低的外援。
数据结构算法也一样,数据结构自身是否能实现算法,自己就能实现,性能效率不是太差的话,肯定优先考虑。自己确实实现不了(也可能是自身经验水平不够,不知道能实现),或者性能比较差,加个数据结构作为变量或者函数辅助,能很轻松实现,并且性能也不错,性价比整体也不差。回报率并不比自身完成差,就行了。商人就爱看回报率是否有得赚,保本小亏也能做,亏损过大肯定不干,早就甩手了!
按难度循序渐进
leetcode 近两千道题目(题目还在增加),茫茫题海,从何刷起?
迷茫,弯路:
- 找题
- 找到了不应该现阶段做的题
- 没有全套的优质题解可以参考
先易后难,循序渐进:
数组-> 链表-> 哈希表->字符串->栈与队列->树->回溯->贪心->动态规划->图论->高级数据结构,再从简单刷起,做了几个类型题目之后,再慢慢做中等题目、困难题目。
即使有这样一个整体规划,对于一位初学者甚至算法老手寻找合适自己的题目也是很困难,时间成本很高,而且题目还不一定就是经典题目。
用最短的时间按照循序渐进的难度顺序把经典题目都做一遍,这样效率才是最高的!
先刷二叉树,先刷二叉树,先刷二叉树!
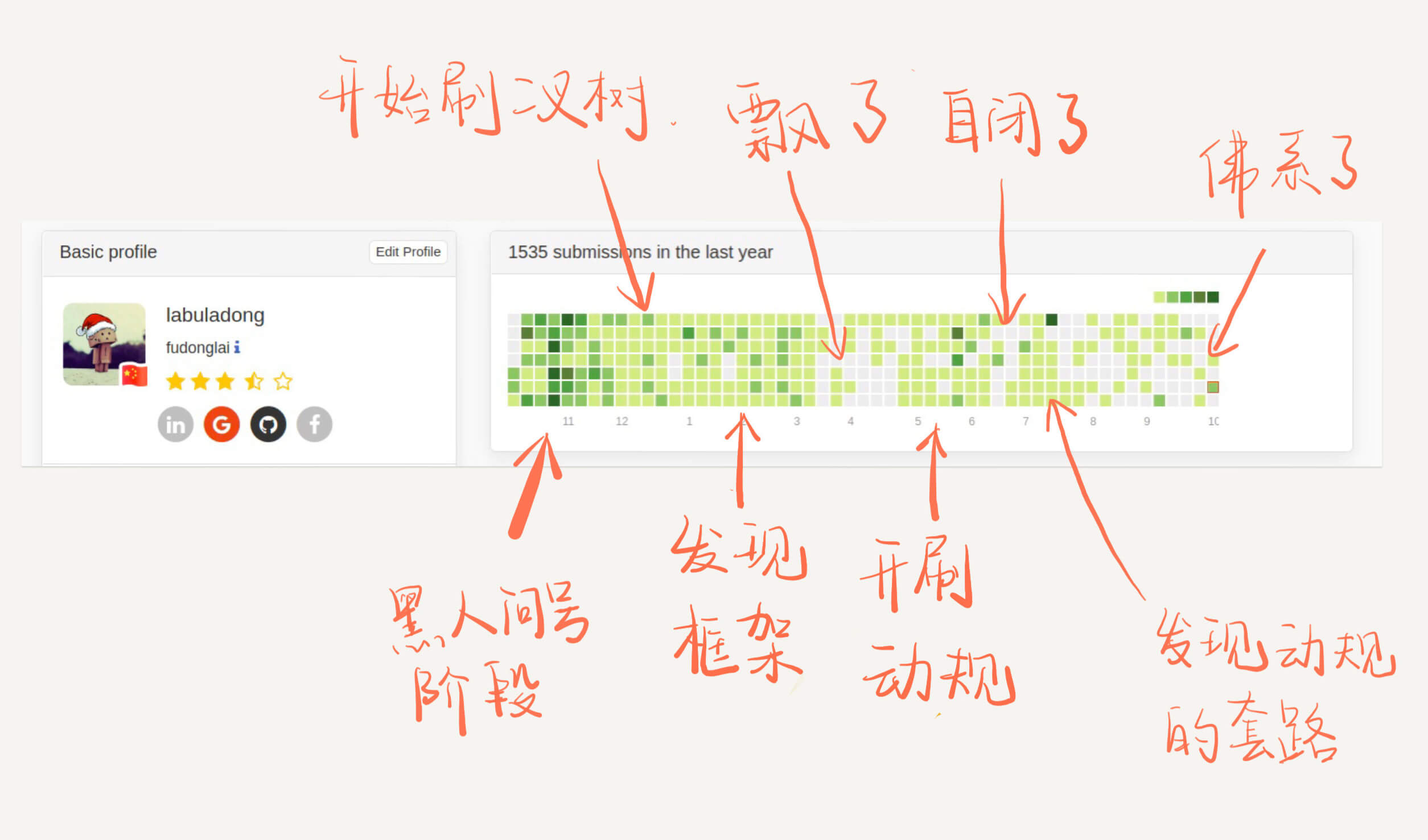
大部分人对数据结构相关的算法文章不感兴趣,而是更关心动规回溯分治等等技巧。为什么要先刷二叉树呢,因为二叉树是最容易培养框架思维的,而且大部分算法技巧,本质上都是树的遍历问题。
不要小看这几行破代码,几乎所有二叉树的题目都是一套这个框架就出来了:
void traverse(TreeNode root) {
// 前序遍历代码位置
traverse(root.left)
// 中序遍历代码位置
traverse(root.right)
// 后序遍历代码位置
}先明确大概的思路,找出规律,再动手写代码
算法,无非就是对各种数据结构、一些数学知识、及编程逻辑的综合运用。算法应用题主要用来锻炼逻辑思维能力,以便在工作中碰到相似的场景,能快速制定实现方案。(缺乏算法训练,并不代表逻辑思维能力障碍,只是比那些有一定训练量的人要薄弱一些。就好像一个人从小体弱多病,排除特殊疾病特例,通常是身体抵抗力弱,完全可以通过后天运动锻炼,达到增强体抗力的目的。算法也一样,只要脑子正常,没有特殊疾病,完全可以通过后天不断训练进行强化。算法应用题做得少,很可能笔试做的算法题都是第一次做,绝大部分人第一次接触新的算法题,都会花很长的时间寻找规律,不断试错,最后才能解出来。)
二叉树前中后序递归遍历;数组、链表、栈、队列保存中间状态信息;for、while 循环处理和优化。
思路:
- 这道题需要用到哪些数据结构、中间存储变量及辅助函数。
- 找出题目规律,数据结构或者数学知识方面的,肯定有一个或多个规律,没有规律则是一个无限不循环的无解问题。
思路刚开始可能并不能保证百分百正确,先有一个大概的思路就行了,有一个循序渐进的过程,大牛也是这样练就成的。
找规律通常需要将抽象的题目,拆解成简单明了的小单元,通过画图辅助,找到小单元的规律;有时候小单元找不到规律,需要将题目整体框架抽取出来,从整体结构主干出发,能发现规律;又或者拆解、整体分析都发现不了,那就黑盒模拟数据测试,反向推导出规律。
数组(Array)
数组的基本概念
数组是一种聚合数据类型,它是将具有相同类型的若干变量有序地组织在一起的集合。数组可以说是最基本的数据结构,在各种编程语言中都有对应。一个数组可以分解为多个数组元素,按照数据元素的类型,数组可以分为整型数组、字符型数组、浮点型数组、指针数组和结构数组等。数组还可以有一维、二维以及多维等表现形式。
数组的类型
一维数组
基本概述
性质特征
定义使用
【Java】
定义:
int[] intArr = new int[10];
int[] intArr2 = {1, 2, 3, 4, 5, 6, 7};
使用:
intArr[0] = 1;
遍历:
for (int i = 0; i < intArr.length; i++) {
// TODO
}
for (int i : intArr) {
// TODO
}优势与缺陷
查找快,增删慢。
数组因为连续存储,有索引定位,查找、更新元素较快。
由于数组长度初始化之后是固定的,删除、新增元素,需要借用到新的数组,并重新调整元素位置和数组长度,性能效率不是很好。
应用场景
二维数组
基本概述
性质特征
定义使用
【Java】
定义:
int cols = 3, rows = 2;
int[][] intArrTwo = new int[cols][rows]; // 三列两行| 0 | 1 | 2 |
|---|---|---|
| 1 |
使用:
intArrTwo[2][1] = 7;| 0 | 1 | 2 |
|---|---|---|
| 1 | 7 |
遍历:
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
System.out.print(intArrTwo[j][i] + " ");
}
System.out.println();
}优势与缺陷
应用场景
多维数组
基本概述
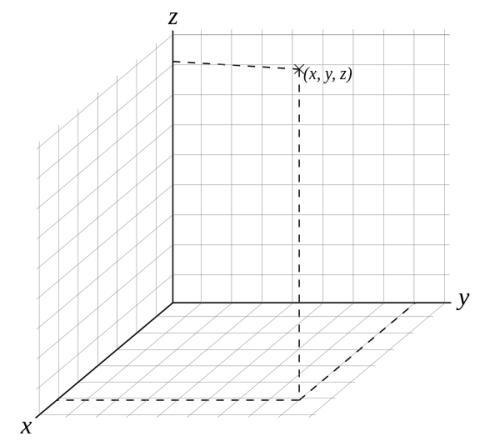
右手定则确定x、y、z轴方向: 在三维坐标系中,Z轴的正轴方向是根据右手定则确定的。右手定则也决定三维空间中任一坐标轴的正旋转方向。 要标注X、Y和Z轴的正轴方向,就将右手背对着屏幕放置,拇指即指向X轴的正方向。伸出食指和中指,如右图所示,食指指向Y轴的正方向,中指所指示的方向即是Z轴的正方向。
性质特征
定义使用
【Java】
定义:
int x = 3, y = 3, z = 3;
int[][][] intArrThree = new int[x][y][z];
int x = 4, y = 4, z = 4, d = 4, s = 5;
int[][][][] intArrFour = new int[x][y][z][d];
int[][][][][] intArrFive = new int[x][y][z][d][s];
使用:
intArrThree[x-1][y-1][z-1] = 7;
遍历:
for (int i = 0; i < z; i++) { // 逐层z 先y后x
for (int j = 0; j < x; j++) {
for (int k = 0; k < y; k++) {
System.out.print(intArrThree[j][k][i] + " ");
}
System.out.println();
}
System.out.println();
}优势与缺陷
应用场景
链表(Linked List)
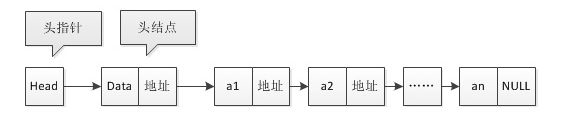
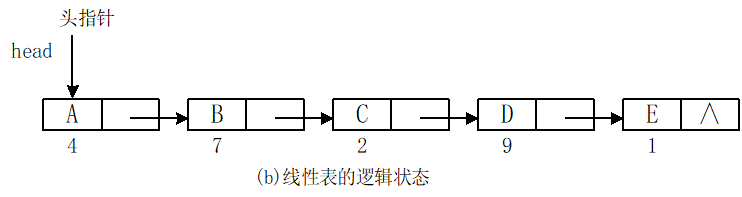
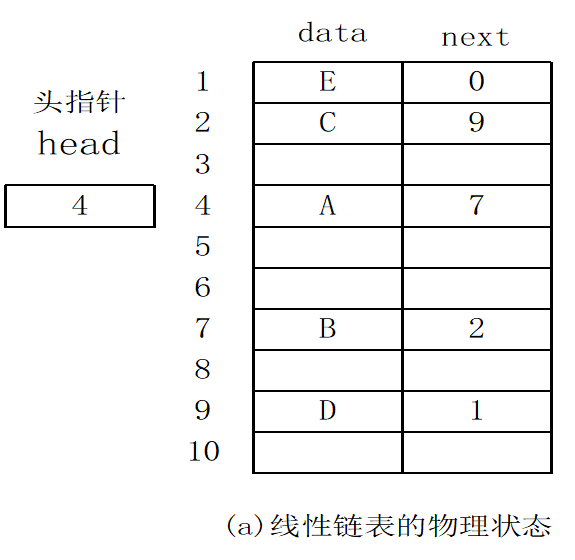
链表是一种数据元素按照链式存储结构进行存储的数据结构,这种存储结构具有在物理上存在非连续的特点。链表由一系列数据结点构成,每个数据结点包括数据域和指针域两部分。其中,指针域保存了数据结构中下一个元素存放的地址。链表结构中数据元素的逻辑顺序是通过链表中的指针链接次序来实现的。
单链表(singly linked list)
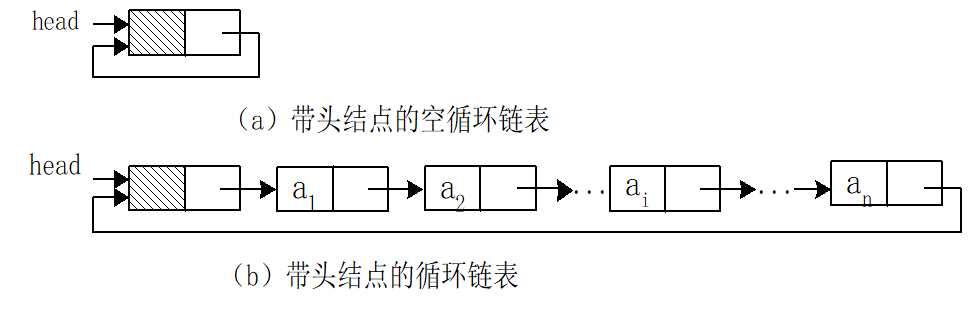
循环链表(circular list)

双链表(doubly linked list)
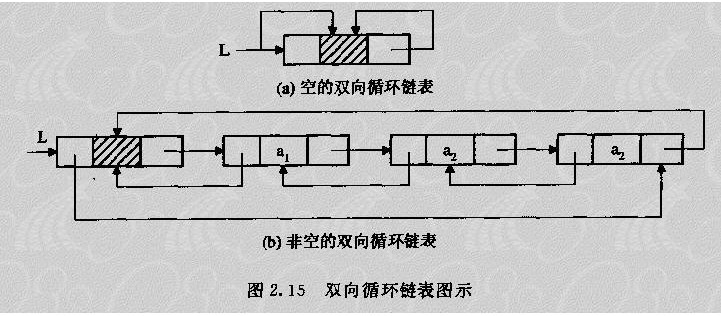
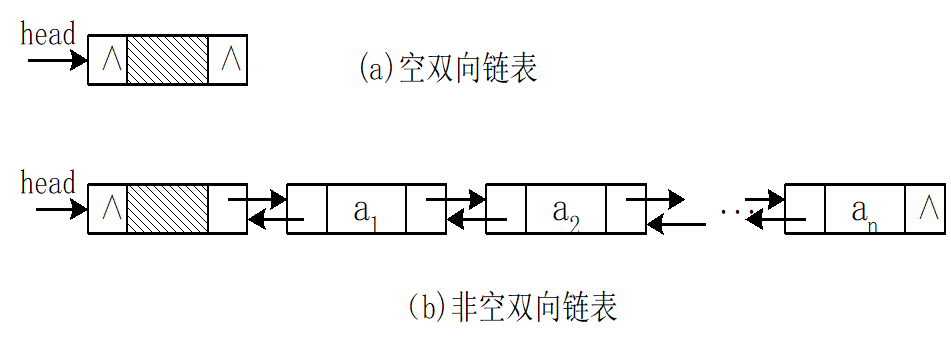
循环双链表(circular doubly linked list)
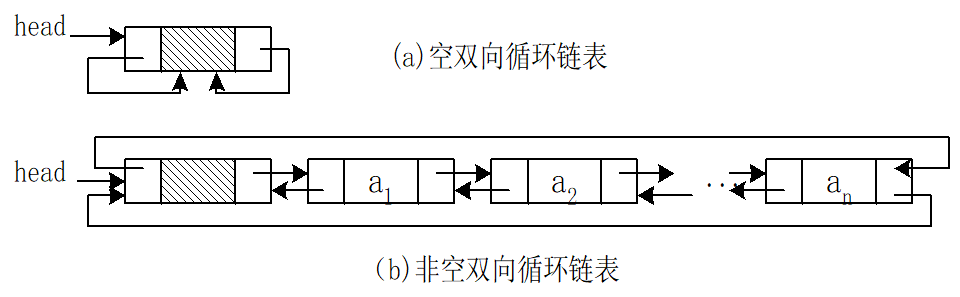
链式存储结构的优缺点
优点:
结点空间可以动态申请和释放。
它的数据元素的逻辑次序靠结点的指针来指示,进行数据插入或删除时不需要移动数据元素。
不足:
每个结点中的指针域需额外占用存储空间,当每个结点的数据域所占字节不多时,指针域所占存储空间的比重就显得很大。
链式存储结构是一种非随机存储结构。对任一结点的操作都要从指针链查找到该结点,这增加了算法的复杂度。
链表算法题
21. 合并两个有序链表(简单)
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
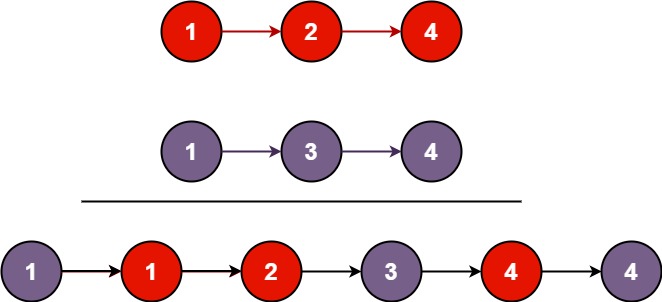
输入:l1 = [1,2,4], l2 = [1,3,4]
输出:[1,1,2,3,4,4]
输入:l1 = [], l2 = []
输出:[]
输入:l1 = [], l2 = [0]
输出:[0]解法:
递归
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if (l1 == null) return l2;
if (l2 == null) return l1;
// 每次比较两个结点,取较小的返回就是了
ListNode min = l1.val < l2.val ? l1 : l2;
// 可以打印一下min结点,打印的结果就是合并后链表顺序
//System.out.print(min.val);
// 小结点后序
min.next = mergeTwoLists(min.next, l1.val >= l2.val ? l1 : l2);
return min;
}
}创建新头节点,循环遍历比较链表结点大小。可能比递归解法好理解一些。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
// 创建新头节点,循环遍历比较两链表结点大小
ListNode tmpHead = new ListNode(0);
ListNode curr = tmpHead;
while (l1 != null && l2 != null) {
if (l1.val < l2.val) {
curr.next = l1;
curr = curr.next;
l1 = l1.next;
} else {
curr.next = l2;
curr = curr.next;
l2 = l2.next;
}
}
// 一条链表为空了,直接指向另一条链表
if (l1 == null) {
curr.next = l2;
} else {
curr.next = l1;
}
return tmpHead.next;
}
}876. 链表的中间结点(简单)
给定一个头结点为 head 的非空单链表,返回链表的中间结点。
如果有两个中间结点,则返回第二个中间结点。
实例:
输入:[1,2,3,4,5]
输出:此列表中的结点 3 (序列化形式:[3,4,5])
返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。
输入:[1,2,3,4,5,6]
输出:此列表中的结点 4 (序列化形式:[4,5,6])
由于该列表有两个中间结点,值分别为 3 和 4,返回第二个结点。解法:
快慢指针
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode middleNode(ListNode head) {
// 额外变量,快慢指针
ListNode fp = head, sp = head;
while (fp != null && fp.next != null) {
fp = fp.next.next;
sp = sp.next;
}
return sp;
}
}栈(Stack)
栈是一种特殊的线性表,它只能在一个表的一个固定端进行数据结点的插入和删除操作。栈按照后进先出的原则来存储数据,也就是说,先插入的数据将被压入栈底,最后插入的数据在栈顶,读出数据时,从栈顶开始逐个读出。栈在汇编语言程序中,经常用于重要数据的现场保护。栈中没有数据时,称为空栈。
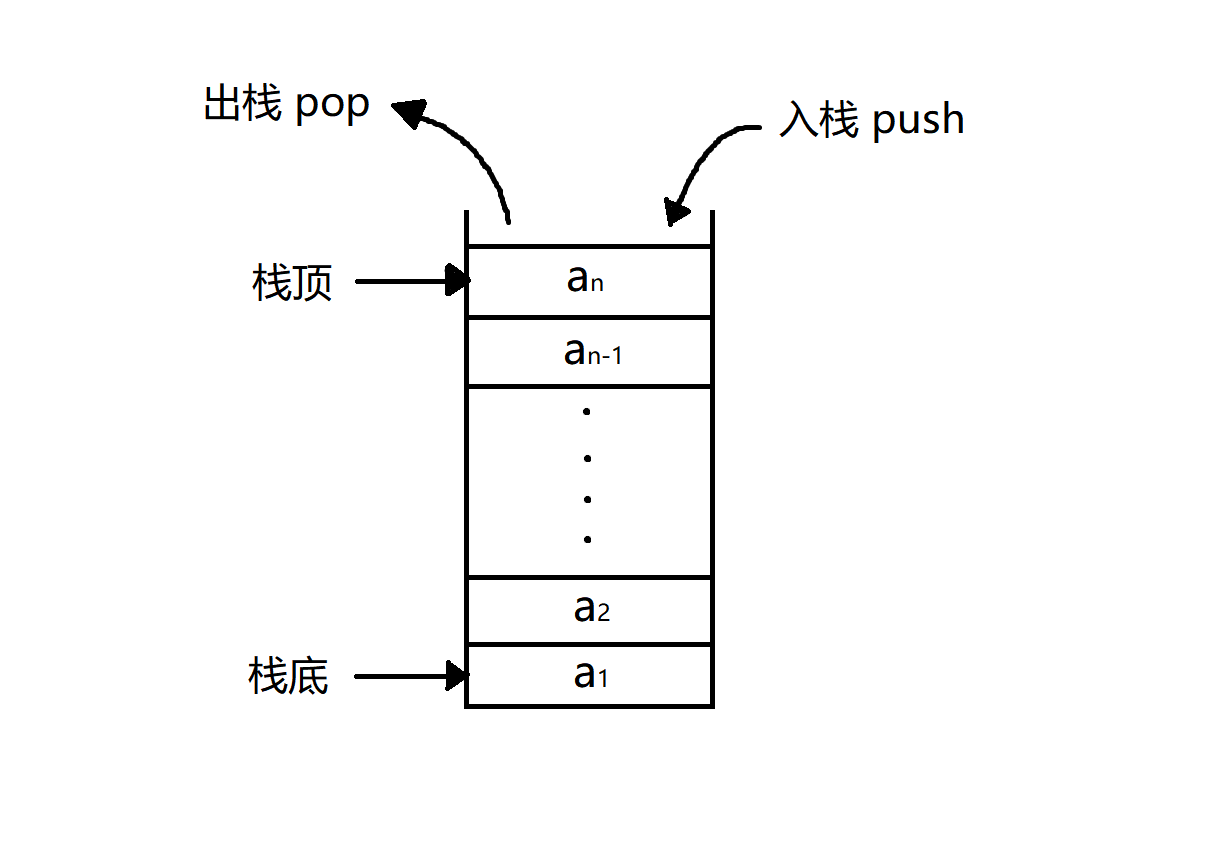
队列(Queue)
队列和栈类似,也是一种特殊的线性表。和栈不同的是,队列只允许在表的一端进行插入操作,而在另一端进行删除操作。一般来说,进行插入操作的一端称为队尾,进行删除操作的一端称为队头。队列中没有元素时,称为空队列。
顺序队列
链式队列
循环队列
树(Tree)
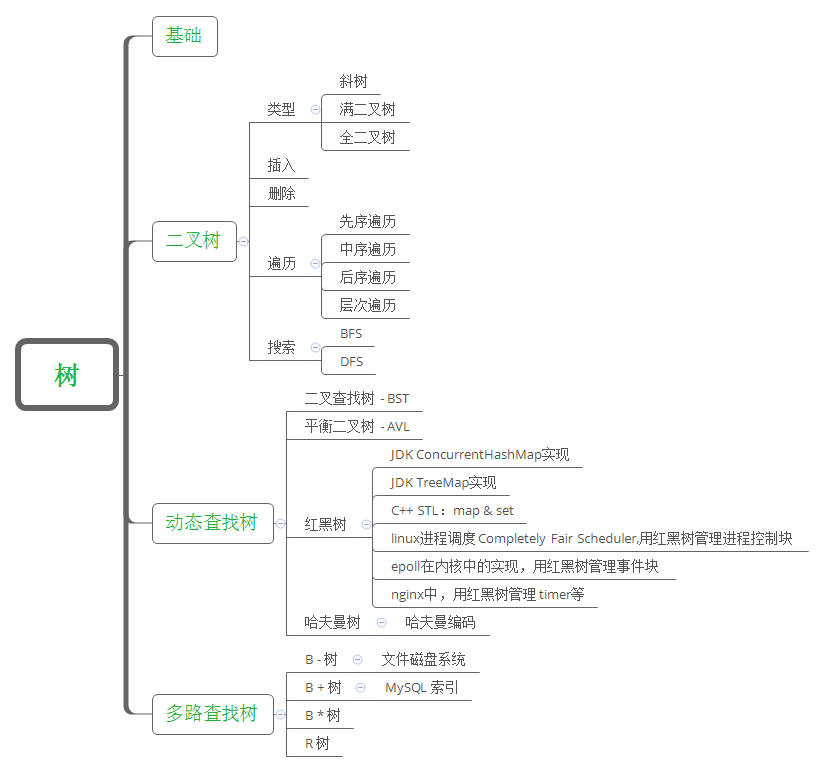
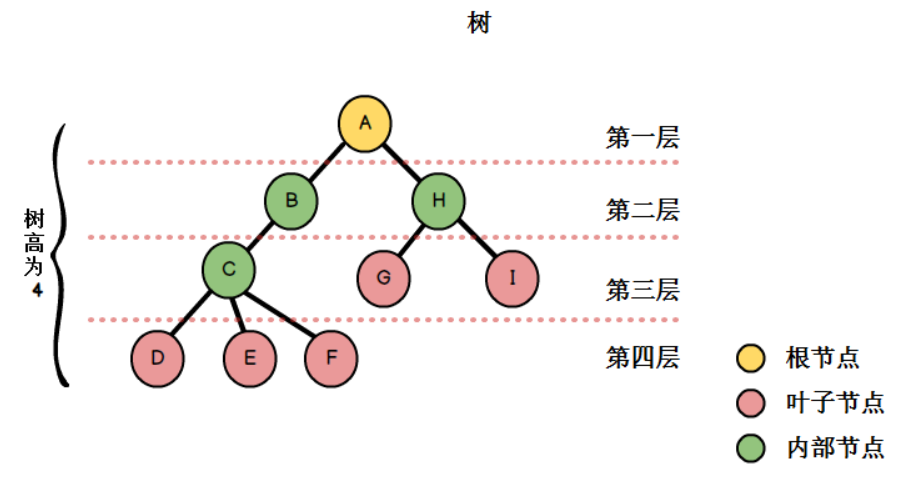
树是典型的非线性结构,它是包括,2个结点的有穷集合K。在树结构中,有且仅有一个根结点,该结点没有前驱结点。在树结构中的其他结点都有且仅有一个前驱结点,而且可以有两个后继结点,m≥0。
树的基本概念
空集合也是树,称为空树。空树中没有结点。
结点的度:一个结点含有的子结点的个数称为该结点的度。
树的度:一棵树中,最大的结点的度称为树的度。
叶结点或终端结点:度为0的结点称为叶结点。
非终端结点或分支结点:度不为0的结点。
双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点。
孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点。
兄弟结点:具有相同父结点的结点互称为兄弟结点。
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推。
树的高度或深度:树中结点的最大层次。
堂兄弟结点:双亲在同一层的结点互为堂兄弟。
结点的祖先:从根到该结点所经分支上的所有结点。
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。
森林:由m(m>=0)棵互不相交的树的集合称为森林。
树的遍历(逐个树递归)
前序遍历(先根遍历):根左右。
中序遍历(中根遍历):左根右。
后序遍历(后根遍历):左右根。
层次遍历:一层一层自左向右。
例题:
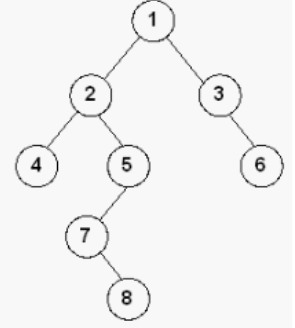
前序遍历结果是:1,2,4,5,7,8,3,6
中序遍历结果是:4,2,7,8,5,1,3,6
后序遍历结果是:4,8,7,5,2,6,3,1
层次遍历结果是:1,2,3,4,5,6,7,8
无序树
树中任意节点的子结点之间没有顺序关系,这种树称为无序树,也称为自由树。
有序树
树中任意节点的子结点之间有顺序关系,这种树称为有序树。
树的类型
二叉树
每个节点最多含有两个子树的树称为二叉树。
满二叉树
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2^k - 1 ,则它就是满二叉树。
完全二叉树
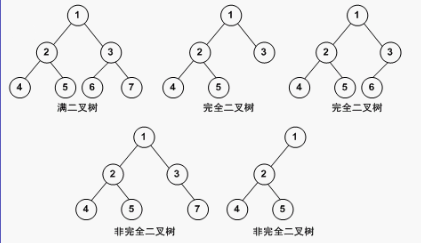
如果对满二叉树的结点进行编号, 约定编号从根结点起, 自上而下, 自左而右。则深度为k的, 有n个结点的二叉树, 当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时, 称之为完全二叉树。
个人理解,将这颗二叉树按从上到下、从左到右的顺序进行编号,空缺的节点也占编号,最后取出非空缺节点的编号,如果编号连续,则是完全二叉树,否则就不是。
从满二叉树和完全二叉树的定义可以看出, 满二叉树是完全二叉树的特殊形态, 即如果一棵二叉树是满二叉树, 则它必定是完全二叉树。
哈夫曼树(Huffman Tree)
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
树的带权路径长度WPL(weighted path length):树中所有叶子结点的带权路径长度之和。

(a)WPL=9x2+4x2+5x2+2x2=18+8+10+4=40
(b)WPL=9x1+5x2+4x3+2x3=9+10+12+6=37
(c)WPL=4x1+2x2+5x3+9x3=4+4+15+27=50
权值越大的结点离根结点越近的二叉树才是最优二叉树。
线索(化)二叉树
在二叉树的结点上加上线索的二叉树称为线索二叉树,对二叉树以某种遍历方式(如先序、中序、后序或层次等)进行遍历,使其变为线索二叉树的过程称为对二叉树进行线索化。
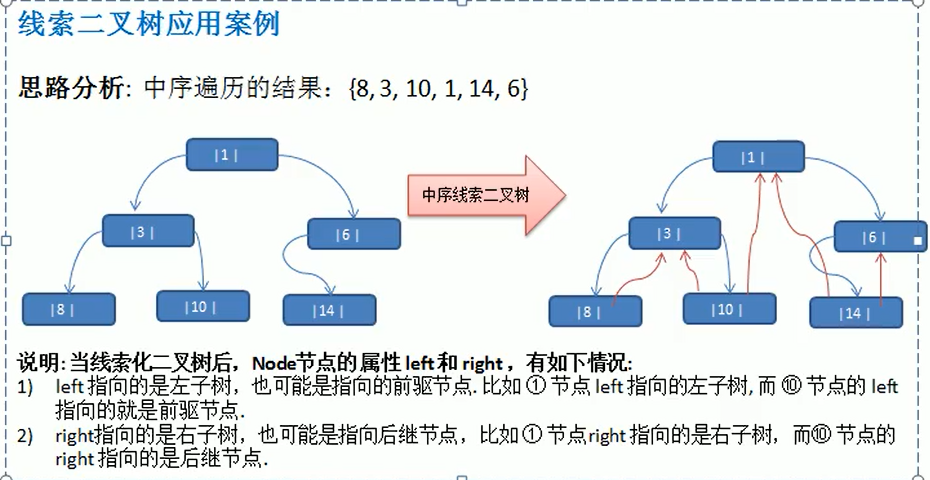
线索化二叉树介绍:
n个节点的二叉树含有n+1【公式 2n-(n-1)=n+1】个空指针域。利用二叉链表中的空指针域,存放指向该节点在某种遍历次序下的前驱和后继节点的指针(这种附加指针称为“线索”)。
这种加上了线索的二叉链表称为线索链表,相应的二叉树称为线索二叉树。根据线索性质的不同,线索二叉树可以分为前序线索二叉树,中序线索二叉树和后序线索二叉树三种。
一个节点的前一个节点,称为前驱节点。
一个节点的后一个节点,称为后继节点。
★二叉排序/查找树(BST/Binary Sort/Search Tree)
基本概述
二叉排序树(Binary Sort Tree),又称二叉查找树(Binary Search Tree),亦称二叉搜索树。
性质特征
一棵空树,或者是具有下列性质的二叉树:
若左子树不空,则左子树上所有结点的值均小于它的根结点的值。
若右子树不空,则右子树上所有结点的值均大于它的根结点的值。
左、右子树也分别为二叉排序树。
没有键值相等的结点。
优势与缺陷
优势
由于数据有序,逐步左右子树二分比较,在大部分情况下,查询效率比单纯的链表和数组的查询效率要高。
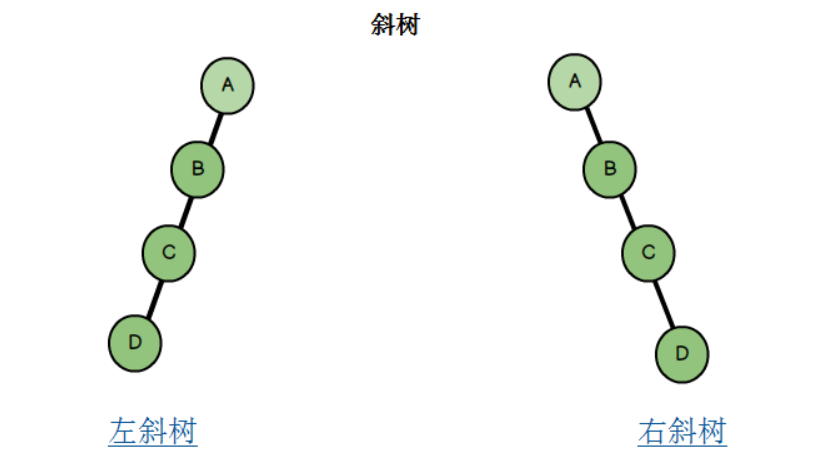
缺陷
所有元素构成左斜树或者右斜树的时候,二叉树变成了单链表形式,查询速度明显降低(因为需要依次比较),不能发挥BST的优势,因为每次还需要比较左子树,其查询速度比单链表还慢。
应用场景
时间复杂度
二叉查找树的时间复杂度就是树的深度(树有几层)。
假设n为每一层节点树,x为树的高度(第几层),则n与x的关系可以表示为:
n = 2^(x-1),把x-1看作X,则
X = log2^n = logn
空间复杂度
★平衡二叉树(AVL树)
基本概述
AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的左右子树的高度差绝对值不超过1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis。
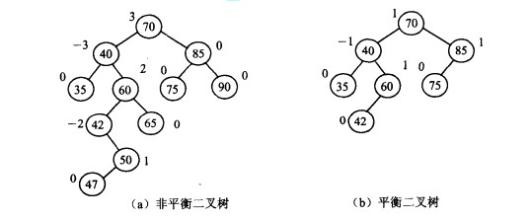
性质特征
AVL树本质上还是一棵二叉搜索树,它的特点是:
- 要么是棵空树,要么其根节点左右子树的深度之差的绝对值不超过1;
- 其左右子树也都是平衡二叉树;
- 二叉树节点的平衡因子定义为该节点的左子树的深度减去右子树的深度。则平衡二叉树的所有节点的平衡因子只可能是-1,0,1。
平衡调整规则
AVL树自平衡旋转规则:
左-左型 右旋
右-右型 左旋
右-左型 先右旋成右-右型,再左旋
左-右型 先左旋成左-左型,再右旋
优势与缺陷
优势
构建AVL树的时候,调整节点的位置,避免出现所有节点构成斜树的情况。
缺陷
二叉树需要加载到内存的,如果二叉树的节点少,没有什么问题,但是如果二叉树的节点很多(比如1亿),就存在如下问题:
问题1:在构建二叉树时,需要多次进行I/O操作(海量数据存在数据库或文件中),节点海量,构建二叉树时,速度有影响。
问题2:节点海量,也会造成二叉树的高度很大,会降低操作速度。
应用场景
节点大小平衡树(Size Balanced Tree)
定义
SBT也是一种自平衡二叉查找树,它的平衡原理是每棵树的大小不小于其兄弟树的子树的大小。
即size(x->l)≥size(x->r->l),size(x->r->r),右边同理size(x->r)≥size(x->l->l),size(x->l->r)
★红黑树(Red Black Tree/R-B Tree)
基本概述
红黑树(Red Black Tree)是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。
红黑树是在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。
红黑树是一种特化的AVL树(平衡二叉树),都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。
它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的:它可以在O(log n)时间内做查找、插入和删除,这里的n是树中元素的数目。
红黑树是一种特定类型的二叉树,它是在计算机科学中用来组织数据比如数字的块的一种结构。若一棵二叉查找树是红黑树,则它的任一子树必为红黑树。
红黑树是一种平衡二叉查找树的变体,它的左右子树高差有可能大于1,所以红黑树不是严格意义上的平衡二叉树(AVL),但对之进行平衡的代价较低,其平均统计性能要强于AVL树。
由于每一颗红黑树都是一颗二叉排序树,因此,在对红黑树进行查找时,可以采用运用于普通二叉排序树上的查找算法,在查找过程中不需要颜色信息。
性质特征
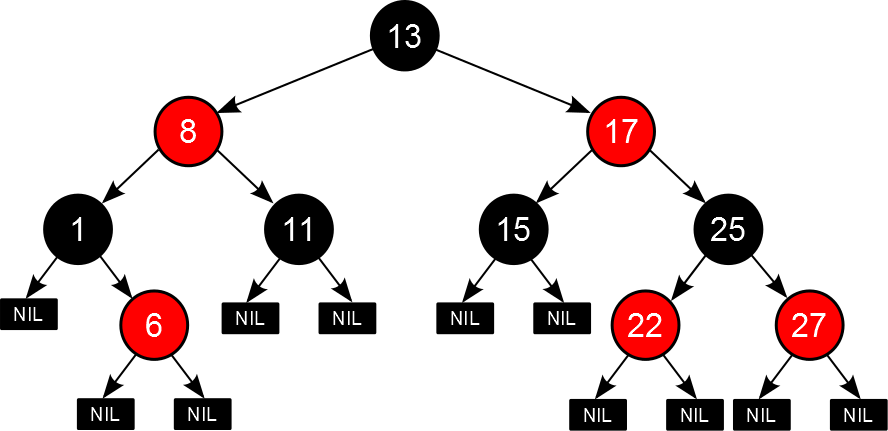
红黑树是每个节点都带有颜色属性的二叉查找树,颜色或红色或黑色。
在二叉查找树强制一般要求以外,对于任何有效的红黑树也还要具备如下性质:
每个节点要么是黑色,要么是红色。(红或黑)
根节点是黑色。 (根黑)
每个叶子节点(NULL/NIL)是黑色。(叶黑)
每个红色节点的两个子节点都是黑色。 (红子黑)
任意路径上不能有两个连续的红色节点。
任意结点到每个叶子结点的路径都包含数量相同的黑结点。(路径下黑相同)
新插入的节点默认为红色。
这些约束强制了红黑树的关键性质:从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。
性质4导致路径上不能有两个连续的红色节点确保了这个结果。最短的可能路径都是黑色节点,最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点,这就表明了没有路径能多于任何其他路径的两倍长。
因为红黑树是一种特化的二叉查找树,所以红黑树上的只读操行与普通二叉查找树相同。
平衡调整规则
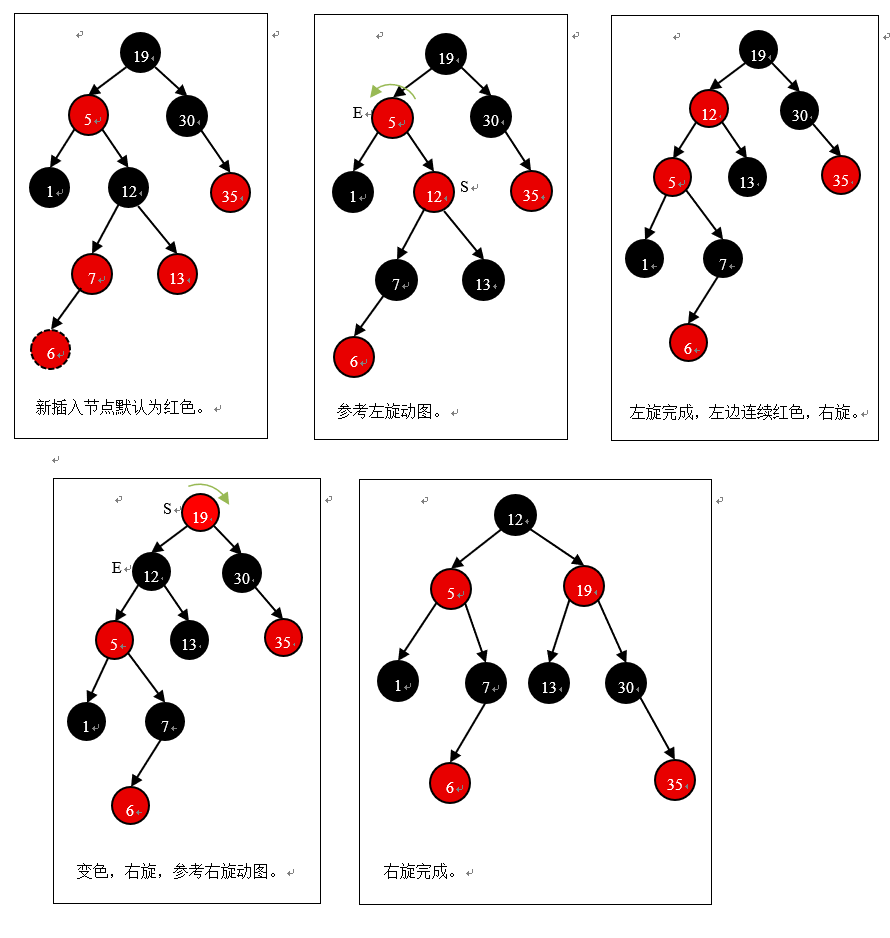
旋转和颜色变换规则:所有新插入的节点默认为红色。
变颜色的情况:当前节点的父节点是红色,切它的祖父(爷爷)节点的另一个子节点(叔叔节点)也是红色。
把父节点变为黑色
把叔叔节点也变为黑色
把祖父(爷爷)节点变为红色
把指针指到祖父(爷爷)节点,设为当前要操作的节点,分析节点变换规则
左旋:当前节点的父节点是红色,叔叔节点是黑色,且当前节点是右子树,把当前节点的父节点设为要操作的节点,左旋。
右旋:当前节点的父节点是红色,叔叔节点是黑色,且当前节点是在左子树,右旋。
把父节点变为黑色
把祖父(爷爷)节点变为红色
以祖父(爷爷)节点旋转
优势与缺陷
应用场景
- Java ConcurrentHashMap & TreeMap
- C++ STL: map & set
- linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块
- epoll在内核中的实现,用红黑树管理事件块
- nginx中,用红黑树管理timer等
时间复杂度
空间复杂度
2-3树
基本概述
性质特征
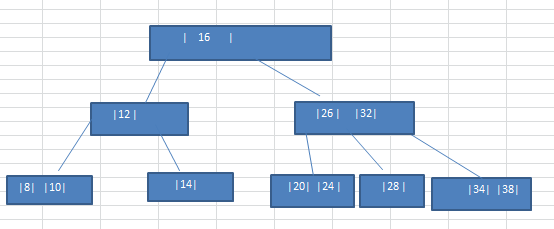
2-3树是最简单的B树结构, 具有如下特点:
2-3树的所有叶子节点都在同一层(只要是B树都满足这个条件)。
2-3树是由二节点和三节点构成的树。
有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点。
有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点。
平衡调整规则
插入规则
当按照性质规则插入一个数到某个节点时,不能满足性质要求,就需要拆,先向上拆,如果上层满,则拆本层,拆后仍然需要满足性质要求。
对于三节点的子树的值大小仍然遵守(BST二叉排序树)的规则。
优势与缺陷
应用场景
2-3-4树
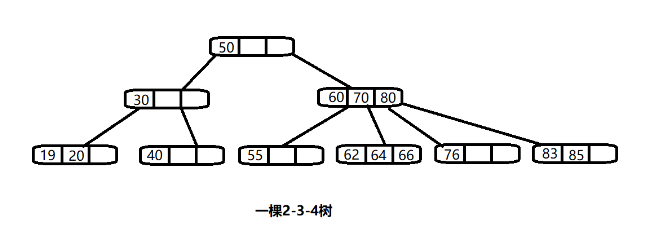
基本概述
性质特征
平衡调整规则
优势与缺陷
应用场景
★B树
基本概述
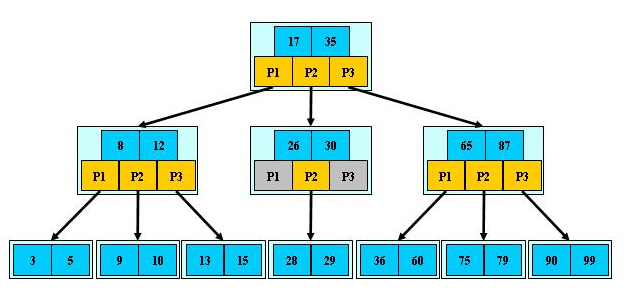
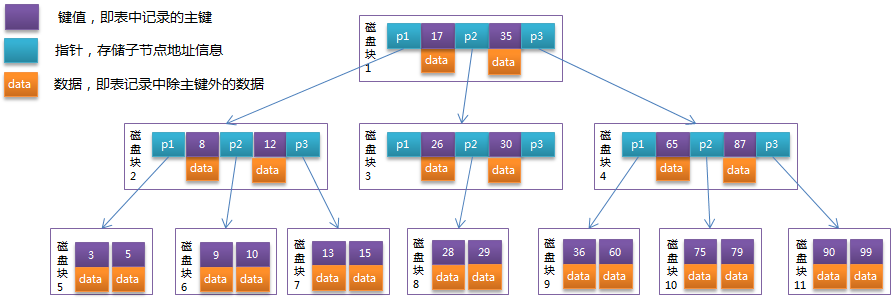
B树(英语: B-tree)是一种自平衡的树,能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作,都在对数时间内完成。B树,概括来说是一种自平衡的m阶树,与自平衡二叉查找树不同,B树适用于读写相对大的数据块的存储系统,例如磁盘。
B树和平衡二叉树稍有不同的是B树属于多叉树又名平衡多路查找树(查找路径不只两个),数据库索引技术里大量使用者B树和B+树的数据结构。
B树的阶:节点的最多子节点个数。比如2-3树的阶是3,2-3-4树的阶是4。
B树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点。
关键字集合分布在整颗树中,即叶子节点和非叶子节点都存放数据。
搜索有可能在非叶子结点结束。
其搜索性能等价于在关键字全集内做一次二分查找。
性质特征
排序方式:所有节点关键字是按递增次序排列,并遵循左小右大原则。
子节点数:非叶节点的子节点数>1,且<=M ,且M>=2,空树除外(注:M阶代表一个树节点最多有多少个查找路径,M=M路,当M=2则是2叉树,M=3则是3叉树)。
关键字数:枝节点的关键字数量大于等于ceil(m/2)-1个且小于等于M-1个(注:ceil()是个朝正无穷方向取整的函数 如ceil(1.1)结果为2)。
所有叶子节点均在同一层、叶子节点除了包含了关键字和关键字记录的指针外也有指向其子节点的指针,只不过其指针地址都为null对应下图最后一层节点的空格子。
简化理解
- 根结点至少有两个子女。
- 每个中间节点都包含k-1个元素和k个孩子,其中 m/2 <= k <= m(m为一个树节点最多有多少个查找路径)
- 每一个叶子节点都包含k-1个元素,其中 m/2 <= k <= m
- 所有的叶子结点都位于同一层。
- 每个节点中的元素从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域分划。
平衡调整规则
优势与缺陷
应用场景
★B+树
基本概述
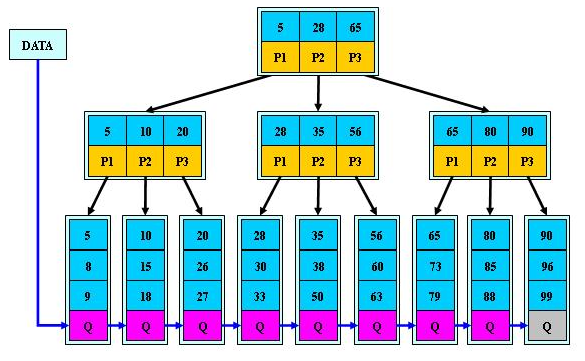
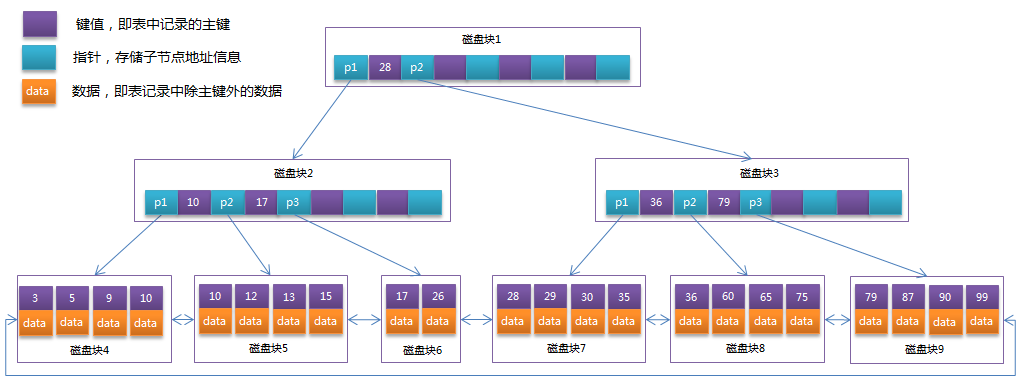
B+树是B树的一个升级版,相对于B树来说B+树更充分的利用了节点的空间,让查询速度更加稳定,其速度完全接近于二分法查找。
B+树的说明
B+树的搜索与B树也基本相同,区别是B+树只有达到叶子结点才命中(B树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找。
所有关键字都出现在叶子结点的链表中(即数据只能在叶子节点【也叫稠密[chóu]索引】),且链表中的关键字(数据)恰好是有序的。
不可能在非叶子结点命中。
非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层。
更适合文件索引系统。
B树和B+树各有自己的应用场景,不能说B+树完全比B树好,反之亦然。
性质特征
B+跟B树不同B+树的非叶子节点不保存关键字记录的指针,只进行数据索引,这样使得B+树每个非叶子节点所能保存的关键字大大增加。
B+树叶子节点保存了父节点的所有关键字记录的指针,所有数据地址必须要到叶子节点才能获取到。所以每次数据查询的次数都一样。
B+树叶子节点的关键字从小到大有序排列,左边结尾数据都会保存右边节点开始数据的指针。
非叶子节点的子节点数=关键字数(来源百度百科)(根据各种资料 这里有两种算法的实现方式,另一种为非叶节点的关键字数=子节点数-1(来源维基百科),虽然他们数据排列结构不一样,但其原理还是一样的Mysql 的B+树是用第一种方式实现)。
特点
B+树的层级更少:相较于B树B+每个非叶子节点存储的关键字数更多,树的层级更少所以查询数据更快。
B+树查询速度更稳定:B+所有关键字数据地址都存在叶子节点上,所以每次查找的次数都相同所以查询速度要比B树更稳定。
B+树天然具备排序功能:B+树所有的叶子节点数据构成了一个有序链表,在查询大小区间的数据时候更方便,数据紧密性很高,缓存的命中率也会比B树高。
B+树全节点遍历更快:B+树遍历整棵树只需要遍历所有的叶子节点即可,而不需要像B树一样需要对每一层进行遍历,这有利于数据库做全表扫描。
B树相对于B+树的优点是,如果经常访问的数据离根节点很近,而B树的非叶子节点本身存有关键字其数据的地址,所以这种数据检索的时候会要比B+树快。
平衡调整规则
优势与缺陷
应用场景
MySQL数据库索引
select * from user where user_id = 100; -- 使用hash的话,hash(100) = 5,则会查到user_id = 5的记录。
select * from user where user_id < 100; -- 使用hash不能进行范围查找,因为需要对每一个user_id计算hash。
select * from user where user_id = 100 and name = ‘大黄’; -- 组合查询
B*树

基本概述
B*树是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针。
B*树的说明
B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3,而B+树的块的最低使用率为B+树的1/2。
从第1个特点可以看出,B*树分配新结点的概率比B+树要低,空间使用率更高。
性质特征
首先是关键字个数限制问题,B+树初始化的关键字初始化个数是cei(m/2),b*树的初始化个数为(cei(2/3*m))。
B+树节点满时就会分裂,而B*树节点满时会检查兄弟节点是否满(因为每个节点都有指向兄弟的指针),如果兄弟节点未满则向兄弟节点转移关键字,如果兄弟节点已满,则从当前节点和兄弟节点各拿出1/3的数据创建一个新的节点出来。
平衡调整规则
优势与缺陷
应用场景
R树
基本概述
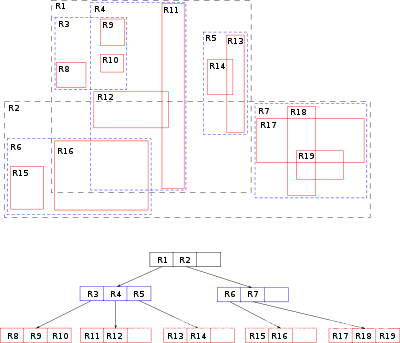
R树是用来做空间数据存储的树状数据结构。例如给地理位置,矩形和多边形这类多维数据建立索引。
R树的核心思想是聚合距离相近的节点并在树结构的上一层将其表示为这些节点的最小外接矩形(MBR),这个最小外接矩形就成为上一层的一个节点。因为所有节点都在它们的最小外接矩形中,所以跟某个矩形不相交的查询就一定跟这个矩形中的所有节点都不相交。叶子节点上的每个矩形都代表一个对象,节点都是对象的聚合,并且越往上层聚合的对象就越多。也可以把每一层看做是对数据集的近似,叶子节点层是最细粒度的近似,与数据集相似度100%,越往上层越粗糙。
性质特征
平衡调整规则
优势与缺陷
应用场景
Trie (前缀)树
基本概述
性质特征
平衡调整规则
优势与缺陷
应用场景
并查集
基本概述
性质特征
平衡调整规则
优势与缺陷
应用场景
二叉树算法题
整体框架思维
class Solution {
// 通常不建议使用外部变量、外部函数,除非算法本身无法实现,必须使用外部变量或函数才能实现,或者使用外部变量性价比更高
// private int count;
// private void connectTwoNode(TreeNode node1, TreeNode node2) {};
public TreeNode invertTree(TreeNode root) {
// 递归结束条件
if (root == null) return root;
// 前序:进下一棵二叉树之前,在当前二叉树要做什么
// 有没有办法减少递归迭代次数?优化性能
invertTree(root.left);
invertTree(root.right);
// 后序:出二叉树之前,要做什么
return root;
}
}226. 翻转二叉树(简单)
考查点:
二叉树前序遍历
翻转一棵二叉树。
示例:
输入:
4
/ \
2 7
/ \ / \
1 3 6 9
输出:
4
/ \
7 2
/ \ / \
9 6 3 1
解法:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) return root;
if (root.left == null && root.right == null) return root;
// 前序:进下一棵二叉树之前,在当前二叉树要做什么
// cunrent node
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
// child node
invertTree(root.left);
invertTree(root.right);
// 后序:出二叉树之前,要做什么
return root;
}
}116. 填充每个节点的下一个右侧节点指针(中等)
考查点:
二叉树前序遍历
添加树节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
进阶:
你只能使用常量级额外空间。 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
示例:
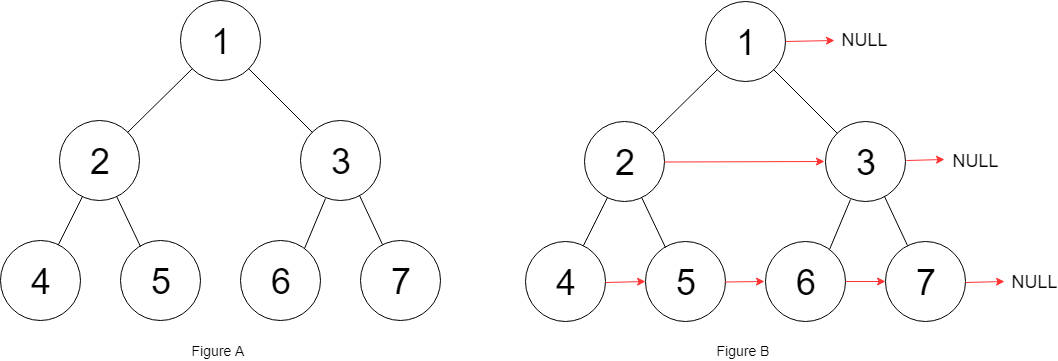
输入:root = [1,2,3,4,5,6,7]
输出:[1,#,2,3,#,4,5,6,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。解法:
/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, Node _left, Node _right, Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
};
*/
class Solution {
public Node connect(Node root) {
// 完全二叉树,左节点为空的话,右节点必然为空,否则不符合完全二叉树规则
if (root == null || root.left == null) return root;
// 前序:进下一棵二叉树之前,在当前二叉树要做什么
// 子节点连接
root.left.next = root.right;
// 建立在root结点已经连接的好了的条件上,操作子节点
if (root.next != null) {
root.right.next = root.next.left;
}
// 前序遍历 根左右
connect(root.left);
connect(root.right);
// 后序:出二叉树之前,要做什么
return root;
}
}114. 二叉树展开为链表(中等)
考查点:
二叉树后序遍历
树节点位置操作
给你二叉树的根结点 root ,请你将它展开为一个单链表:
展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。 展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:
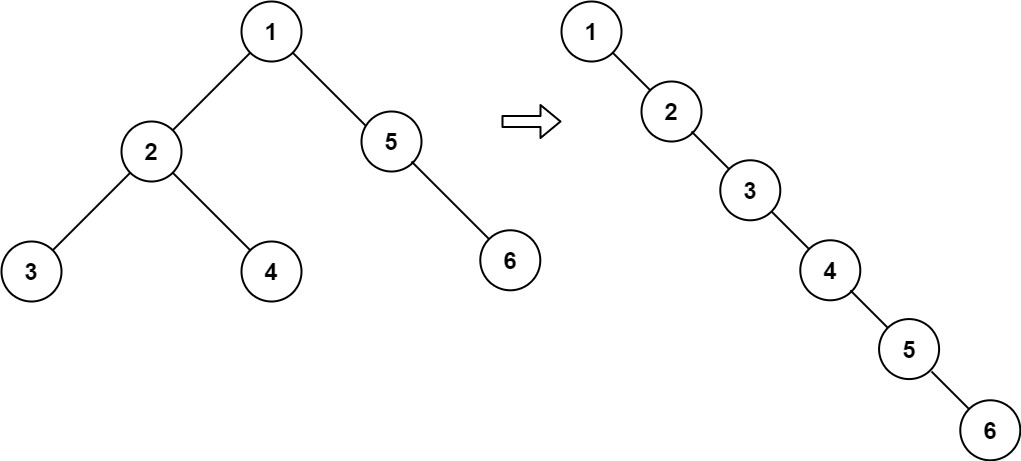
输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]解法:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public void flatten(TreeNode root) {
if (root == null) return;
// 前序:进下一棵二叉树之前,在当前二叉树要做什么
// 这题不需要做什么
flatten(root.left);
flatten(root.right);
// 后序:出二叉树之前,要做什么
// 需要交换左右位置,并且把交换后的左子树添加到右子树末端
if (root.left != null) {
// 交换子树
TreeNode tmp = root.right;
root.right = root.left;
root.left = tmp;
// 移至右子树末端
TreeNode lr = root.right;
while(lr.right != null) lr = lr.right;
lr.right = root.left;
// 记得左子树指向null
root.left = null;
}
}
}222. 完全二叉树的节点个数(中等)
考查点:
二叉树前序遍历
完全二叉树、满二叉树性质
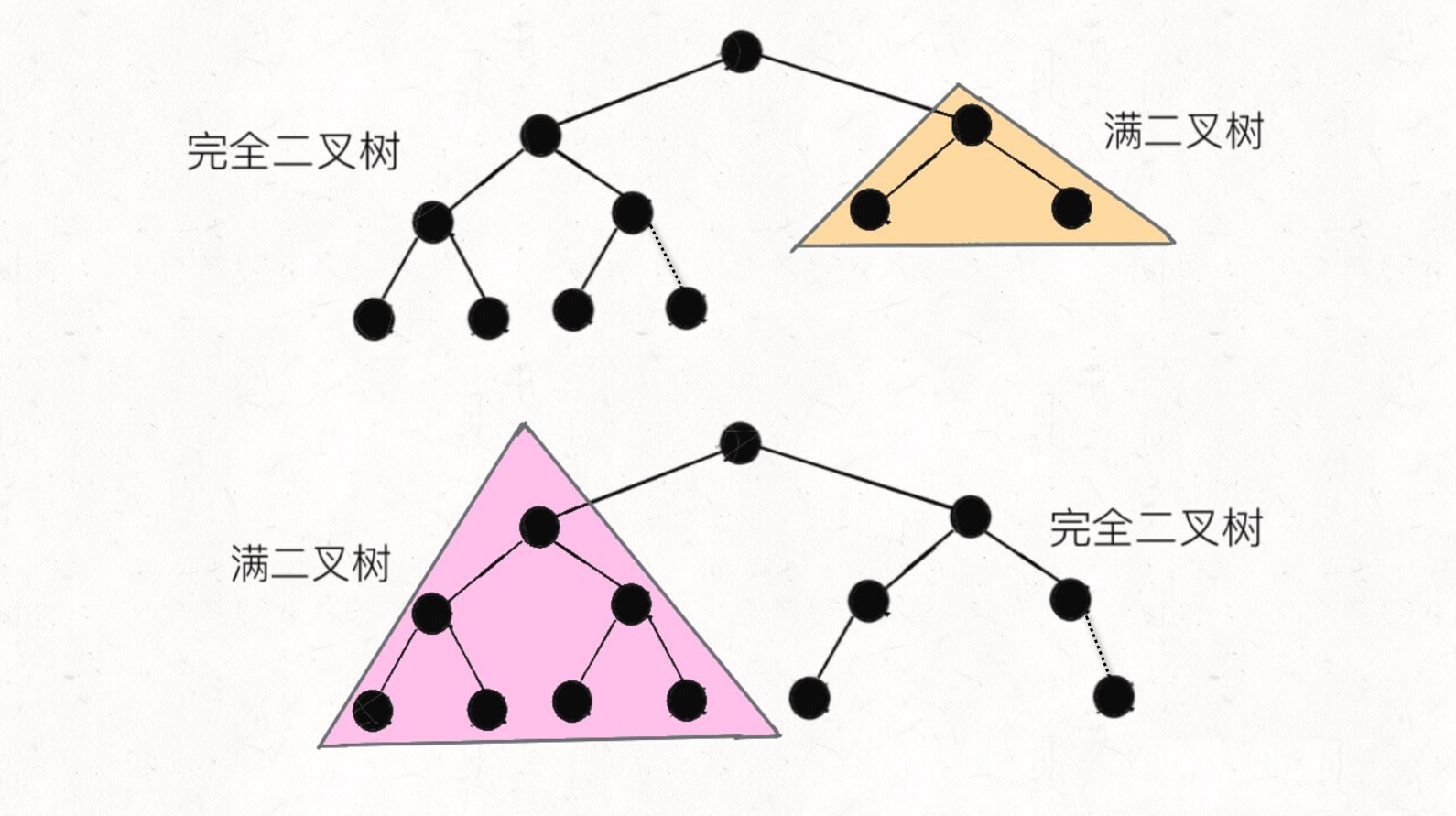
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例 1:
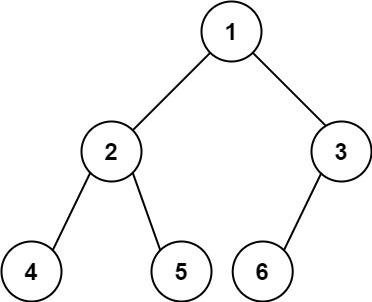
输入:root = [1,2,3,4,5,6]
输出:6思路:
比较左子树的高度,利用满二叉树性质(2^k-1)优化。
左右子树高度相同,左子树一定是满二叉树,右子树需要进一步判断;
左右子树高度不相同,右子树一定是满二叉树,左子树需要进一步判断。
解法1:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int countNodes(TreeNode root) {
if (root == null) return 0;
return 1 + countNodes(root.left) + countNodes(root.right);
}
}解法2:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int countNodes(TreeNode root) {
if (root == null) return 0;
// 满二叉树性质优化(2^k-1),减少递归迭代次数
int ld = getDepth(root.left);
int rd = getDepth(root.right);
if (ld == rd) { // 左子树为满二叉树,右子树是否满,需要进一步判断
//return 1 + (1 << ld - 1) + countNodes(root.right);
return (1 << ld) + countNodes(root.right);
} else { // 右子树为满二叉树,左子树需要进一步判断
return (1 << rd) + countNodes(root.left);
}
}
private int getDepth(TreeNode node) {
int depth = 0;
while (node != null) {
depth++;
node = node.left;
}
return depth;
}
}654. 最大二叉树(中等)
考查点:
二叉树前序遍历
数组构造指定条件二叉树
给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的 最大二叉树 定义如下:
二叉树的根是数组 nums 中的最大元素。 左子树是通过数组中 最大值左边部分 递归构造出的最大二叉树。 右子树是通过数组中 最大值右边部分 递归构造出的最大二叉树。 返回有给定数组 nums 构建的 最大二叉树 。
示例 1:
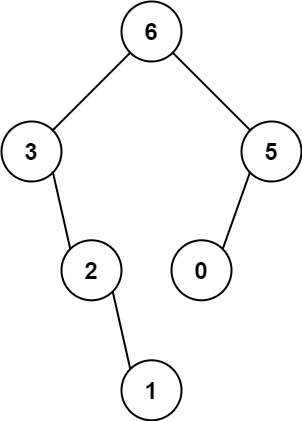
输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。解法:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode constructMaximumBinaryTree(int[] nums) {
return build(nums, 0, nums.length - 1);
}
private TreeNode build(int[] nums, int start, int end) {
// 递归结束条件
if (nums.length < 1 || start > end || start > nums.length - 1) return null;
// 前序,先处理再进入递归
// 找出数组中的最大值
int idx = start, maxVal = nums[idx];
for (int i = start + 1; i <= end; i++) {
if (nums[i] > maxVal) {
idx = i;
maxVal = nums[i];
}
}
// 构造树
TreeNode root = new TreeNode(maxVal);
root.left = build(nums, start, idx - 1);
root.right = build(nums, idx + 1, end);
return root;
}
}105. 从前序与中序遍历序列构造二叉树(中等)
考查要点:
二叉树前序、中序遍历
结果反向构造二叉树
给定一棵树的前序遍历 preorder 与中序遍历 inorder。请构造二叉树并返回其根节点。
示例 1:
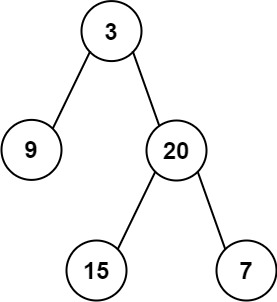
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]解法:
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
return helper(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
}
public TreeNode helper(int[] preorder, int preLeft, int preRight,
int[] inorder, int inLeft, int inRight) {
// 递归终止条件
if (inLeft > inRight || preLeft > preRight) return null;
// val 为前序遍历第一个的值,也即是根节点的值
// idx 为根据根节点的值来找中序遍历的下标
int idx = inLeft, val = preorder[preLeft];
TreeNode root = new TreeNode(val);
for (int i = inLeft; i <= inRight; i++) {
if (inorder[i] == val) {
idx = i;
break;
}
}
// 根据 idx 来递归找左右子树
root.left = helper(preorder, preLeft + 1, preLeft + (idx - inLeft),
inorder, inLeft, idx - 1);
root.right = helper(preorder, preLeft + (idx - inLeft) + 1, preRight,
inorder, idx + 1, inRight);
return root;
}
}106. 从中序与后序遍历序列构造二叉树(中等)
根据一棵树的中序遍历与后序遍历构造二叉树。
注意: 你可以假设树中没有重复的元素。
例如,给出
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]返回如下的二叉树:
3
/ \
9 20
/ \
15 7
解法:
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
return buildTree1(inorder, 0, inorder.length, postorder, 0, postorder.length);
}
public TreeNode buildTree1(int[] inorder, int inLeft, int inRight,
int[] postorder, int postLeft, int postRight) {
// 没有元素了
if (inRight - inLeft < 1) {
return null;
}
// 只有一个元素了
if (inRight - inLeft == 1) {
return new TreeNode(inorder[inLeft]);
}
// 后序数组postorder里最后一个即为根结点
int rootVal = postorder[postRight - 1];
TreeNode root = new TreeNode(rootVal);
int rootIndex = 0;
// 根据根结点的值找到该值在中序数组inorder里的位置
for (int i = inLeft; i < inRight; i++) {
if (inorder[i] == rootVal) {
rootIndex = i;
}
}
// 根据rootIndex划分左右子树
root.left = buildTree1(inorder, inLeft, rootIndex,
postorder, postLeft, postLeft + (rootIndex - inLeft));
root.right = buildTree1(inorder, rootIndex + 1, inRight,
postorder, postLeft + (rootIndex - inLeft), postRight - 1);
return root;
}
}根据前序和后序是否能构造二叉树?
前序和中序可以唯一确定一颗二叉树。
后序和中序可以唯一确定一颗二叉树。
那么前序和后序可不可以唯一确定一颗二叉树呢?
**前序和后序不能唯一确定一颗二叉树!**因为没有中序遍历无法确定左右部分,也就是无法分割。
举一个例子:
tree1 tree2
1 1
/ \
2 2
/ \
3 3tree1 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
tree2 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
那么tree1 和 tree2 的前序和后序完全相同,这是一棵树么,很明显是两棵树!
所以前序和后序不能唯一确定一颗二叉树!
652. 寻找重复的子树(中等)
考查要点:
二叉树的后序遍历
子树存储和比较
给定一棵二叉树,返回所有重复的子树。对于同一类的重复子树,你只需要返回其中任意一棵的根结点即可。
两棵树重复是指它们具有相同的结构以及相同的结点值。
示例 1:
1
/ \
2 3
/ / \
4 2 4
/
4下面是两个重复的子树:
2
/
4和
4你需要以列表的形式返回上述重复子树的根结点。
解法:
class Solution {
// 记录所有的子树和出现的次数
HashMap<String, Integer> memo = new HashMap<>();
// 记录重复子树的根节点
LinkedList<TreeNode> res = new LinkedList<>();
public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
traverse(root);
return res;
}
private String traverse(TreeNode root) {
// 递归到叶子节点了
if (root == null) return "#";
String left = traverse(root.left);
String right = traverse(root.right);
// 后序遍历代码
// 使用StringBuilder是因为它的速度快,在不用考虑线程安全的前提下推荐使用这个
StringBuilder sb = new StringBuilder();
// 拼接子树和根节点
sb.append(left).append(",").append(right).append(",").append(root.val);
// 可以获取字符串在map中的值,不存在就新增这个字符串到map中并附值为0
int num = memo.getOrDefault(sb.toString(), 0);
// 无论相同子树重复几次都只会被加入到结果集一次
if (num == 1) res.add(root);
// 子树结果加一
memo.put(sb.toString(), num + 1);
return sb.toString();
}
}堆(Heap)
堆是一种特殊的树形数据结构,一般讨论的堆都是二叉堆。堆的特点是根结点的值是所有结点中最小的或者最大的,并且根结点的两个子树也是一个堆结构。
散列表/哈希表(Hash table)
散列表源自于散列函数(Hash function),其思想是如果在结构中存在关键字和T相等的记录,那么必定在F(T)的存储位置可以找到该记录,这样就可以不用进行比较操作而直接取得所查记录。
图(Graph)
基础概述
图是另一种非线性数据结构。在图结构中,数据结点一般称为顶点,而边是顶点的有序偶对。如果两个顶点之间存在一条边,那么就表示这两个顶点具有相邻关系。
遍历(BFS & DFS)
广度优先搜索(Breadth First Search)
从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止。
换句话说,广度优先搜索遍历图的过程是以v为起点,由近至远,依次访问和v有路径相通且路径长度为1,2...的顶点。
BFS 问题的本质就是让你在一幅「图」中找到从起点 start 到终点 target 的最近距离,这个例子听起来很枯燥,但是 BFS 算法问题其实都是在干这个事儿。
BFS 找到的路径一定是最短的,但代价就是空间复杂度可能比 DFS 大很多。
思维框架
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
Queue<Node> q; // 核心数据结构
Set<Node> visited; // 避免走回头路
q.offer(start); // 将起点加入队列
visited.add(start);
int step = 0; // 记录扩散的步数
while (q not empty) {
int sz = q.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
/* 划重点:这里判断是否到达终点 */
if (cur is target)
return step;
/* 将 cur 的相邻节点加入队列 */
for (Node x : cur.adj())
if (x not in visited) {
q.offer(x);
visited.add(x);
}
}
/* 划重点:更新步数在这里 */
step++;
}
}队列 q 就不说了,BFS 的核心数据结构;cur.adj() 泛指 cur 相邻的节点,比如说二维数组中,cur 上下左右四面的位置就是相邻节点;visited 的主要作用是防止走回头路,大部分时候都是必须的,但是像一般的二叉树结构,没有子节点到父节点的指针,不会走回头路就不需要 visited。
深度优先搜索(Depth First Search)
深度优先搜索是一个递归的过程。其实 DFS 算法就是回溯算法。
假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
最小生成树(Prim & Kruskal)
最短路径(Dijkstra & Frolyd)
拓扑排序(Topological sort)
AOE & 关键路径
算法基础
算法学习建议参考(有血的教训)
由浅入深,逐步加强,不断完善。像婴儿学步、学讲话一样,尊重自然规律。
明确学习目的和目标。比如为了面试要准备到什么程度?deadline之前有多少准备时间?又或是作为编程思维能力像家常便饭一样每天练习。友情提示,离职后,各项技术准备时间最长不要超过三个月,最好是两个月以内。超过三个月的准备期,日常生活饮食和作息习惯很可能会变得一团糟,加上身边的朋友不理解,没人帮助、倾诉,这个过程非常的孤独空虚!很容易就会沉迷不良的诱惑(烟酒、游戏、短视频、影视、综艺)!这些上瘾的行为,一旦沾上,大脑多巴胺分泌机制会导致上瘾,一停下来就很难受,然后不顾一切地迫切渴望更多的愉悦刺激,即使知道是短暂虚拟的,最后陷入长时间的恶性循环,难以自拔!只有触碰到死亡危机线了,大脑开始思考死亡避免方案了,才开始清醒过来,啊,原来自己已经荒废那么长的宝贵时光了!真的,准备期不能超过三个月!慎独!!要工作有收入!!!
对算法感兴趣、喜欢算法、爱上算法。把学算法比作追女孩,自然是有好感、喜欢才会去追,不喜欢的女生可能你连看都不愿意看一眼吧。怎么追呢?第一步是不是要找机会接近认识啊,你都不认识,谈什么深入交流?从认识开始,日常联系聚会玩耍进一步了解,这个过程可能很漫长,可能女孩并不喜欢你,终止你的接触,你能怎么办啊,只能重新去追求其他有好感的女孩了。就好像你学算法很多次想要放弃一样,算法是女孩,每个人对算法的理解不一样,所以算法可以是各种类型的女孩,总之,女孩你肯定是要追的,算法肯定是要学的(针对从事编程开发工作人员,算法是必学的加分项,即使工作不常用,但内卷严重)。可能学算法比追女孩要更容易呢。
兴趣成果驱动,理论概念驱不动,前提饭碗得保住。成天一个劲地看别人总结的经验技巧,看很多遍脑袋可能还是蒙的!从做第一道题开始练习实践,认识了女孩,却不敢主动找人家聊天?不敢邀请她聚会玩耍?自卑退缩?永远走不出第一步,最后的剧情都能想到,很悲惨的结局。
用进废退,工作可能很少用到,但也要抽时间每天或经常练习。一是强化理解,避免遗忘;二是保持稳定的水平,跳槽期间不用花很长时间弥补;三是帮助深入理解编程的本质,更好地理解框架底层实现原理,同时提升自身造轮子的技术水平。
时间复杂度
常见的时间复杂度量级有:
- 常数阶O(1)
- 对数阶O(logN)
- 线性阶O(n)
- 线性对数阶O(nlogN)
- 平方阶O(n²)
- 立方阶O(n³)
- K次方阶O(n^k)
- 指数阶(2^n)
上面从上至下依次的时间复杂度越来越大,执行的效率越来越低。

常数阶 O(1)
int i = 1;
int j = 2;
++i;
j++;
int m = i + j;无论代码执行了多少行,只要是没有循环等复杂结构,它消耗的时候并不随着某个变量的增长而增长,那么无论这类代码有多长,即使有几万几十万行,都可以用O(1)来表示它的时间复杂度。
线性阶 O(n)
for(i=1; i<=n; ++i)
{
j = i;
j++;
}这段代码,for循环里面的代码会执行n遍,因此它消耗的时间是随着n的变化而变化的,因此这类代码都可以用O(n)来表示它的时间复杂度。
对数阶 O(logN)
int i = 1;
while(i<n)
{
i = i * 2;
}从上面代码可以看到,在while循环里面,每次都将 i 乘以 2,乘完之后,i 距离 n 就越来越近了。我们试着求解一下,假设循环x次之后,i 就大于 2 了,此时这个循环就退出了,也就是说 2 的 x 次方等于 n,那么 x = log2^n 也就是说当循环 log2^n 次以后,这个代码就结束了。因此这个代码的时间复杂度为:O(logn)
线性对数阶 O(nlogN)
for(m=1; m<n; m++)
{
i = 1;
while(i<n)
{
i = i * 2;
}
}将时间复杂度为O(logn)的代码循环N遍,时间复杂度就是 n * O(logN),也就是了O(nlogN)。
平方阶 O(n²)
平方阶O(n²) 其实就是把 O(n) 的代码再嵌套循环一遍,它的时间复杂度就是 O(n²) 了。
for(x=1; i<=n; x++)
{
for(i=1; i<=n; i++)
{
j = i;
j++;
}
}这段代码其实就是嵌套了2层n循环,它的时间复杂度就是 O(n*n),即 O(n²)
如果将其中一层循环的n改成m,即:
for(x=1; i<=m; x++)
{
for(i=1; i<=n; i++)
{
j = i;
j++;
}
}那它的时间复杂度就变成了 O(m*n)
空间复杂度
算法稳定性
假设在数列中存在 a[i]=a[j],若在排序之前,a[i]在a[j]前面;并且排序之后,a[i]仍然在a[j]前面。则这个排序算法是稳定的。
常见排序算法
学习排序 - 动画展示排序(opens new window)
整体性比较好系列 - @skywang12345(opens new window)
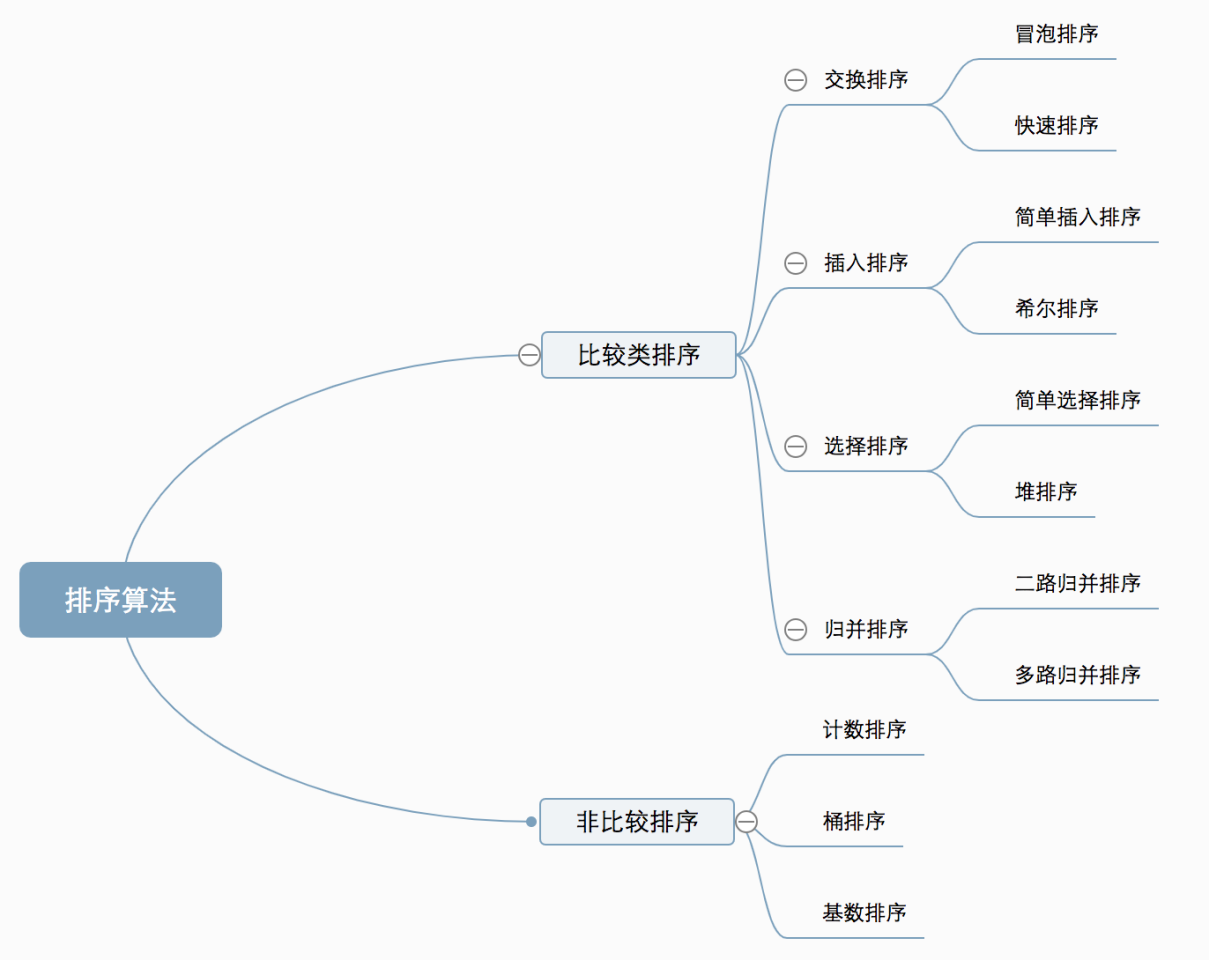
常见排序算法可以分为两大类:
比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
算法复杂度比较
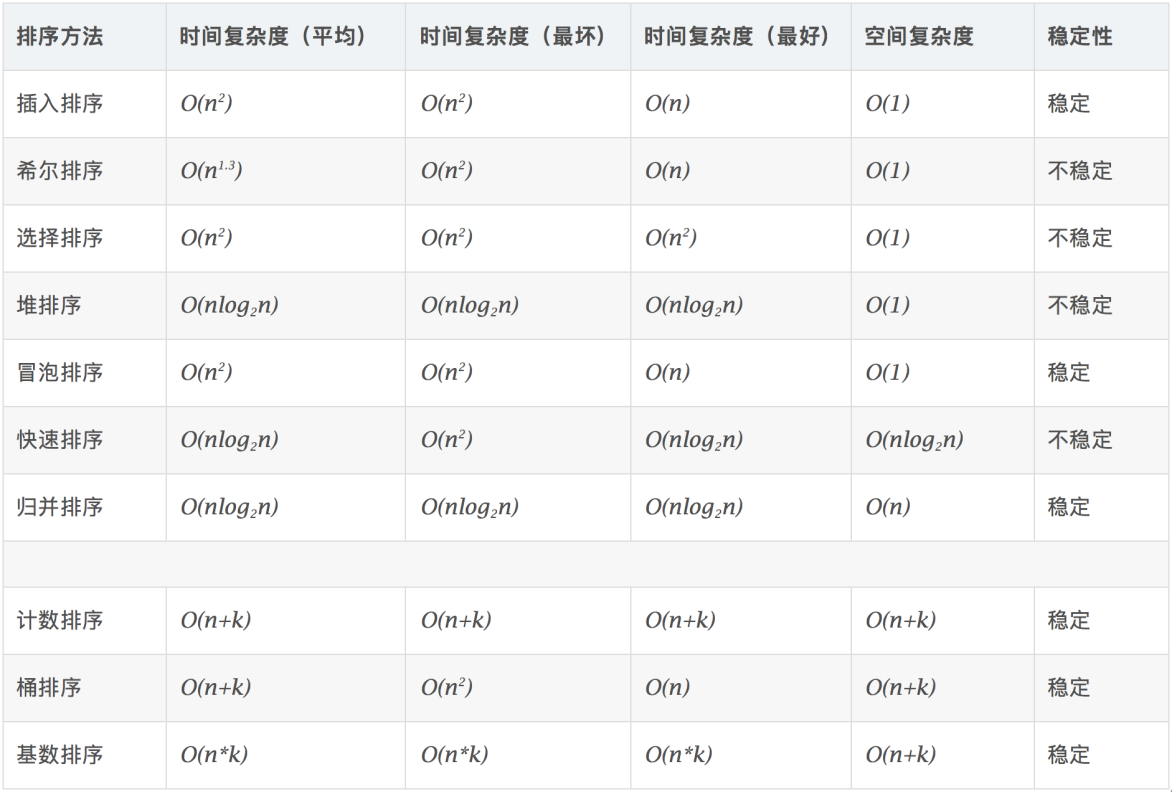
相关概念
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
冒泡排序(bubbleSort)
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,以此比较两个元素,如果它们的顺序(如从大到小、首字母从Z到A)错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
较大的数往后移,就好像水里往上冒的气泡,越往上气泡越大,冒泡排序,越大的数越往后。
算法原理(逻辑思路)
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
时间复杂度
若文件的初始状态是正序的,一趟扫描即可完成排序。所需的关键字比较次数C和记录移动次数M均达到最小值:Cmin = n-1,Mmin = 0。
所以,冒泡排序最好的时间复杂度为O(n)。
若初始文件是反序的,需要进行n-1趟排序。每趟排序要进行n-i次关键字的比较(1≤i≤n-1),且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下,比较和移动次数均达到最大值:
Cmax = n(n-1)/2 = O(n^2)
Cmax = 3n(n-1)/2 = O(n^2)
冒泡排序的最坏时间复杂度为O(n^2)。
因此冒泡排序总的平均时间复杂度为O(n^2)。
空间复杂度
算法稳定性
冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较,交换也发生在这两个元素之间。所以,如果两个元素相等,是不会再交换的;如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法。
实现代码
// 冒泡排序(大的往后,内控结尾): 相邻元素两两比较,因此最后一项不用比较,大的往后放。第一次完毕,最大值在最后面(最后一位索引)
// 要你写这种死记逻辑代码的公司,基本都不是什么好公司,不用写,庆幸你没被他们看中吧!代码优化
针对问题:
数据的顺序排好之后,冒泡算法仍然会继续进行下一轮的比较,直到arr.length-1次,后面的比较没有意义的。
方案:
设置标志位flag,如果发生了交换flag设置为true;如果没有交换就设置为false。
这样当一轮比较结束后如果flag仍为false,即:这一轮没有发生交换,说明数据的顺序已经排好,没有必要继续进行下去。
优化后代码:
应用场景
选择排序(selectSort)
选择排序是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
算法原理(逻辑思路)
n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下:
初始状态:无序区为R[1..n],有序区为空;
第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1..i-1]和R(i..n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
n-1趟结束,数组有序化了。
时间复杂度
空间复杂度
算法稳定性
选择排序是稳定的算法,因为比较相等的时候,可以不交换。
实现代码
// 选择排序(小的往前,内控开头):从0索引开始,依次和后面元素比较,小的往前放,第一次完毕,最小值出现在了最小索引处代码优化
应用场景
▲快速排序(quickSort)
快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
算法原理(逻辑思路)
基本思想:
先从数列中取出一个数作为基准数。
分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
再对左右区间重复第二步,直到各区间只有一个数。
个人理解:取开头基准数,头尾哨兵,挖坑填数+分治法。开头一般放比基准数小的数,所以尾部哨兵找小的数,头部哨兵找大的数,逐个填坑。
以一个数组作为示例,取区间第一个数为基准数。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 72 | 6 | 57 | 88 | 60 | 42 | 83 | 73 | 48 | 85 |
初始时,i = 0; j = 9; X = a[i] = 72
由于已经将a[0]中的数保存到X中,可以理解成在数组a[0]上挖了个坑,可以将其它数据填充到这来。
从j开始向前找一个比X小或等于X的数。当j=8,符合条件,将a[8]挖出再填到上一个坑a[0]中。a[0]=a[8]; i++; 这样一个坑a[0]就被搞定了,但又形成了一个新坑a[8],这怎么办了?简单,再找数字来填a[8]这个坑。这次从i开始向后找一个大于X的数,当i=3,符合条件,将a[3]挖出再填到上一个坑中a[8]=a[3]; j--;
数组变为:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 48 | 6 | 57 | 88 | 60 | 42 | 83 | 73 | 88 | 85 |
i = 3; j = 7; X=72
再重复上面的步骤,先从后向前找,再从前向后找。
从j开始向前找,当j=5,符合条件,将a[5]挖出填到上一个坑中,a[3] = a[5]; i++;
从i开始向后找,当i=5时,由于i==j退出。
此时,i = j = 5,而a[5]刚好又是上次挖的坑,因此将X填入a[5]。
数组变为:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 48 | 6 | 57 | 42 | 60 | 72 | 83 | 73 | 88 | 85 |
可以看出a[5]前面的数字都小于它,a[5]后面的数字都大于它。因此再对a[0…4]和a[6…9]这二个子区间重复上述步骤就可以了。
对挖坑填数进行总结
i =L; j = R; 将基准数挖出形成第一个坑a[i]。
j--由后向前找比它小的数,找到后挖出此数填前一个坑a[i]中。
i++由前向后找比它大的数,找到后也挖出此数填到前一个坑a[j]中。
再重复执行2,3二步,直到i==j,将基准数填入a[i]中。
时间复杂度
空间复杂度
算法稳定性
实现代码
public class QuickSort {
public static void main(String[] args) {
int[] arr = {5, 1, 7, 8, 2, 4, 0, 3 ,7, 1, 9};
System.out.println(Arrays.toString(arr));
//Arrays.sort(arr);
quickSort(arr,0,arr.length - 1);
System.out.println(Arrays.toString(arr));
}
public static void quickSort(int[] arr, int start, int end) {
// 参数校验
if (arr == null || arr.length < 1) {
System.out.println("arr is invalid.");
return;
}
if (start > end || start >= arr.length || end >= arr.length) {
System.out.println("start or end is invalid.");
return;
}
if (start == end) {
return;
}
if (arr.length == 1) {
return;
}
// 排序逻辑
// 选择开头的数作为基准数
int pick = arr[start];
// 定义高低位两个哨兵
int low = start;
int high = end;
// 循环挖坑填数
while (low < high) {
while (low < high && arr[high] >= pick) {
high--;
}
arr[low] = arr[high];
while (low < high && arr[low] <= pick) {
low++;
}
arr[high] = arr[low];
}
arr[low] = pick;
// 递归分治
// 比基准数小的一边
quickSort(arr, start, low);
// 比基准数大的一边
quickSort(arr, low + 1, end);
}
}代码优化
应用场景
▲插入排序(insertSort)
插入排序的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
算法原理(逻辑思路)
从第一个元素开始,该元素可以认为已经被排序;
取出下一个元素,在已经排序的元素序列中从后向前扫描;
如果该元素(已排序)大于新元素,将该元素移到下一位置;
重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
将新元素插入到该位置后;
重复步骤2~5。
文字步骤挺绕脑袋的,直接看动图更容易理解。
其实就是打牌,按顺序排好,新抓的牌跟手上已有的牌比较,放入顺序正确的位置即可。
时间复杂度
空间复杂度
算法稳定性
直接插入排序是稳定的算法,因为在比较相等后,在后面插入。
实现代码
代码优化
插入排序,当最后插入一个最小的数时,需要逐个移动,效率较低。
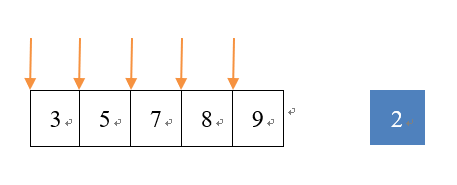
应用场景
希尔排序(shellSort)
1959年Shell发明,第一个突破O(n^2)的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
算法原理(逻辑思路)
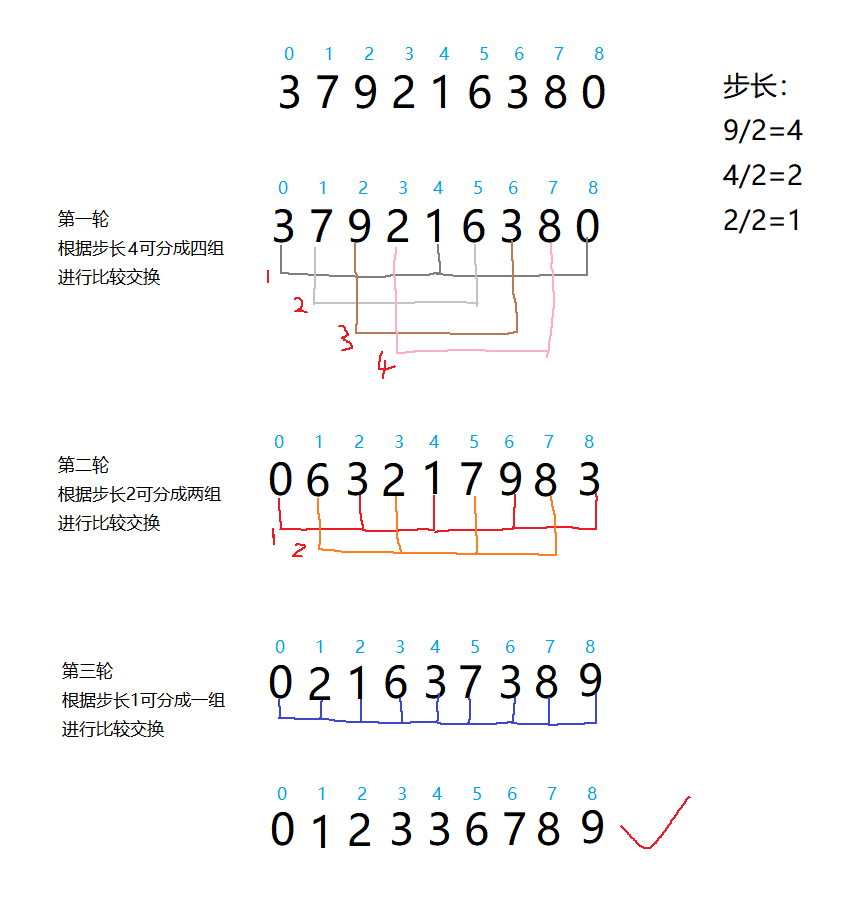
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,具体算法描述:
选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
按增量序列个数k,对序列进行k 趟排序;
每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
时间复杂度
空间复杂度
算法稳定性
实现代码
代码优化
应用场景
▲归并排序(mergeSort)
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
算法原理(逻辑思路)
把长度为n的输入序列分成两个长度为n/2的子序列;
对这两个子序列分别采用归并排序;
将两个排序好的子序列合并成一个最终的排序序列。
个人理解:
将一个无序的数组逐步二分拆分,拆到每个数组只有一个元素,再两两数组合并比较。
时间复杂度
空间复杂度
算法稳定性
实现代码
代码优化
应用场景
▲堆排序(heapSort)
堆排序是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
算法原理(逻辑思路)
基于二叉排序树实现。
将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
时间复杂度
空间复杂度
算法稳定性
实现代码
代码优化
应用场景
计数排序(countingSort)
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
算法原理(逻辑思路)
找出待排序的数组中最大和最小的元素;
统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
时间复杂度
空间复杂度
算法稳定性
实现代码
代码优化
应用场景
桶排序(bucketSort)
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。桶排序的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排)。
算法原理(逻辑思路)
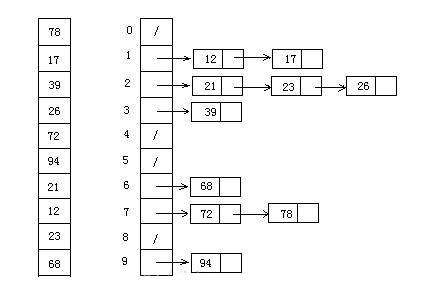
设置一个定量的数组当作空桶;
遍历输入数据,并且把数据一个一个放到对应的桶里去;
对每个不是空的桶进行排序;
从不是空的桶里把排好序的数据拼接起来。
时间复杂度
空间复杂度
算法稳定性
实现代码
代码优化
应用场景
基数排序(radixSort)
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。
算法原理(逻辑思路)
取得数组中的最大数,并取得位数;
arr为原始数组,从最低位开始取每个位组成radix数组;
对radix进行计数排序(利用计数排序适用于小范围数的特点)。
时间复杂度
空间复杂度
算法稳定性
实现代码
代码优化
应用场景
总结
不同情况下排序选择
在不同的情形下,排序速度前三名也不尽相同:
| 排序场景 | 排序效率 |
|---|---|
| Random 随机数 | 希尔>快排>归并 |
| Few unique 多重复 | 快排>希尔>归并 |
| Reversed 反向 | 快排>希尔>归并 |
| Almost sorted 接近顺序 | 插入排序>基数排序>快排>希尔>归并 |
快速排序和希尔排序在排序速度上表现是比较优秀的,而归并排序稍微次之。
查找算法
二分查找
/**
* 二分查找的前提:有序、不重复(数据重复没意义)
*/
public class HalfSearch {
public static void main(String[] args) {
int[] arr = {5, 1, 7, 8, 2, 4, 0, 3 , 6, 9};
System.out.println(Arrays.toString(arr));
QuickSort.sort(arr);
System.out.println(Arrays.toString(arr));
// 二分查找 7
System.out.println(search(arr, 7));
}
/**
* 实现代码,画出操作图很容易就写出来
*/
public static int search(int[] arr, int pick) {
// 参数校验...
// 查找逻辑
int start = 0;
int end = arr.length - 1;
int mid = arr.length / 2;
// 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
while (start <= end) {
if (arr[mid] == pick) { // 找到了,返回下标
return mid;
} else if (arr[mid] > pick) { // 中间数比查找的数大,说明查找的数在左边
end = mid - 1;
mid = (start + end) / 2;
} else { // 中间数比查找的数小,说明查找的数在右边
start = mid + 1;
mid = (start + end) / 2;
}
}
// 没找到,返回-1
return -1;
}
}递归
汉诺塔
斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家莱昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 3,n ∈ N*)。
实现代码
/**
* 斐波那契数列(Fibonacci sequence)
* 0 1 2 3 5 8 13 21 34 55 89 144 ...
* F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N)
*/
public class FiboSequence {
public static void main(String[] args) {
System.out.println(getFiboResult(12));
}
public static int getFiboResult(int n) {
// 参数校验...
// 查找逻辑
if (n == 0)
return 0;
if (n == 1)
return 1;
return getFiboResult(n - 1) + getFiboResult(n - 2);
}
}算法思想
分治算法
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可得到原问题的解。
大事化小,小事化了。
处理事情的方法可以是递归,也可以是循环。
动态规划
求最值,不一定是最优解,也可以是最合适解。
动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,希望找到具有最优值的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
既然是要求最值,核心问题是什么呢?求解动态规划的核心问题是穷举。因为要求最值,肯定要把所有可行的答案穷举出来,然后在其中找最值。
动态规划这么简单,就是穷举就完事了?我看到的动态规划问题都很难啊!
首先,动态规划的穷举有点特别,因为这类问题存在「重叠子问题」,如果暴力穷举的话效率会极其低下,所以需要「备忘录」或者「DP table」来优化穷举过程,避免不必要的计算。
而且,动态规划问题一定会具备「最优子结构」,才能通过子问题的最值得到原问题的最值。
另外,虽然动态规划的核心思想就是穷举求最值,但是问题可以千变万化,穷举所有可行解其实并不是一件容易的事,只有列出正确的「状态转移方程」,才能正确地穷举。
以上提到的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。在实际的算法问题中,写出状态转移方程是最困难的,这也就是为什么很多朋友觉得动态规划问题困难的原因,这里提供我研究出来的一个思维框架,辅助你思考状态转移方程:
明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义。
按上面的套路走,最后的结果就可以套这个框架:
## 初始化 base case
dp[0][0][...] = base
## 进行状态转移
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...] = 求最值(选择1,选择2...)具体来说,动态规划的一般流程就是三步:暴力的递归解法 -> 带备忘录的递归解法 -> 迭代的动态规划解法。
就思考流程来说,就分为一下几步:找到状态和选择 -> 明确 dp 数组/函数的定义 -> 寻找状态之间的关系。
斐波那契数列问题
主要是弄明白什么是重叠子问题(斐波那契数列没有求最值,所以严格来说不是动态规划问题)。
凑零钱问题
主要是集中于如何列出状态转移方程。
背包问题
贪婪算法
保证每次操作都是局部最优的,并且最后得到的结果是全局最优的。
集合覆盖问题
二分法
搜索算法
回溯算法
解决一个回溯问题,实际上就是一个决策树的遍历过程。
基本思路
路径:也就是已经做出的选择。
选择列表:也就是你当前可以做的选择。
结束条件:也就是到达决策树底层,无法再做选择的条件。
代码方面,回溯算法的框架:
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」。
摊还分析
聚合分析
核算法
势能法
动态表
二项队列
斜堆
斐波那契堆
伸展树
一些领域算法
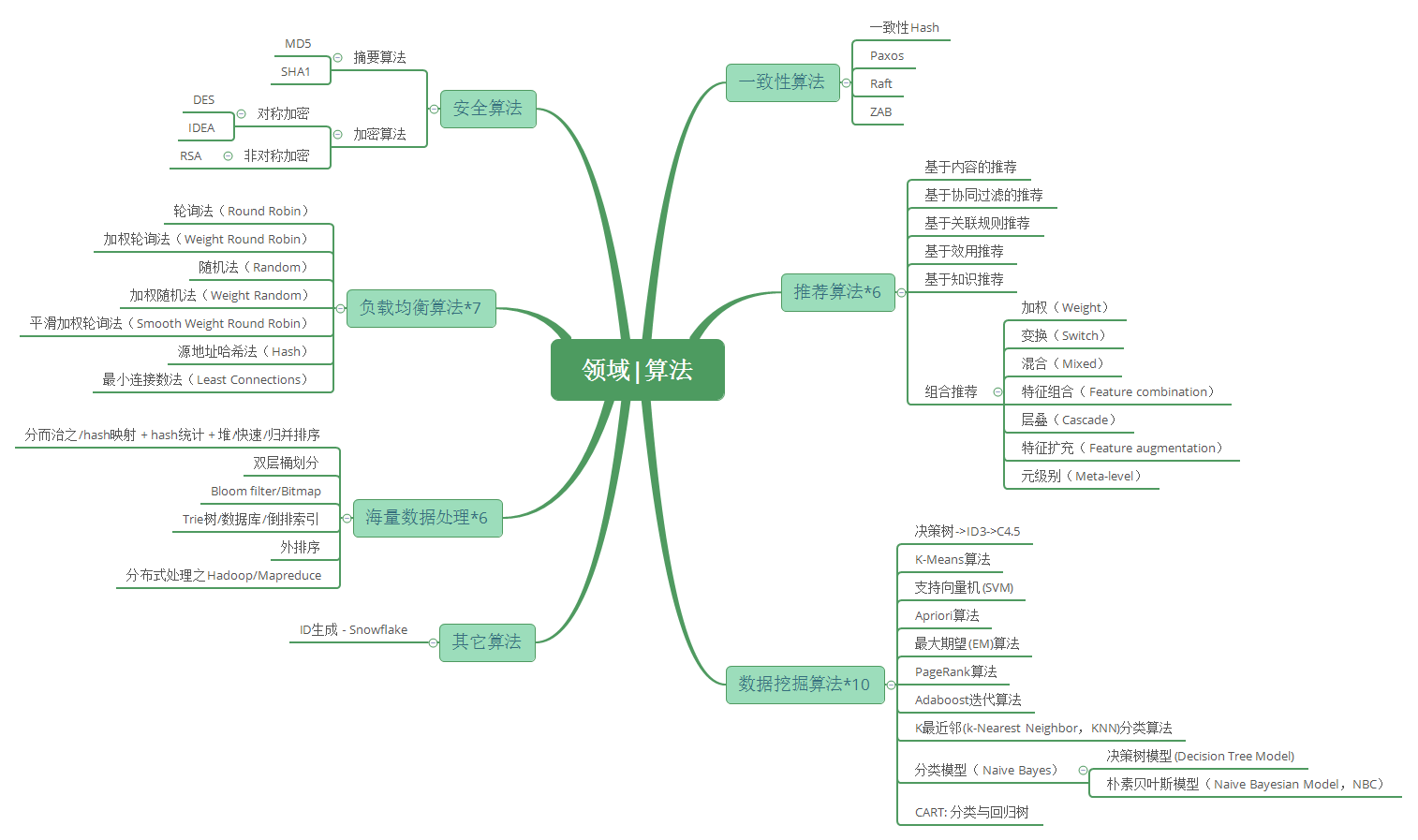
安全算法
字符串匹配
模式预处理:朴素算法(Naive)(暴力破解)
模式预处理:KMP 算法(Knuth-Morris-Pratt)
模式预处理:BM 算法 (Boyer-Moore)
文本预处理:后缀树(Suffix Tree)
大数据处理
分治/hash/排序
分而治之/hash映射 + hash统计 + 堆/快速/归并排序,说白了,就是先映射,而后统计,最后排序:
分而治之/hash映射: 针对数据太大,内存受限,只能是: 把大文件化成(取模映射)小文件,即16字方针: 大而化小,各个击破,缩小规模,逐个解决hash_map统计: 当大文件转化了小文件,那么便可以采用常规的hash_map(ip,value)来进行频率统计。堆/快速排序: 统计完了之后,便进行排序(可采取堆排序),得到次数最多的IP。
案例分析
海量日志数据,提取出某日访问百度次数最多的那个IP
分析: “首先是这一天,并且是访问百度的日志中的IP取出来,逐个写入到一个大文件中。注意到IP是32位的,最多有个2^32个IP。同样可以采用映射的方法,比如%1000,把整个大文件映射为1000个小文件,再找出每个小文中出现频率最大的IP(可以采用hash_map对那1000个文件中的所有IP进行频率统计,然后依次找出各个文件中频率最大的那个IP)及相应的频率。然后再在这1000个最大的IP中,找出那个频率最大的IP,即为所求。”
关于本题,还有几个问题,如下:
- Hash取模是一种等价映射,不会存在同一个元素分散到不同小文件中的情况,即这里采用的是mod1000算法,那么相同的IP在hash取模后,只可能落在同一个文件中,不可能被分散的。因为如果两个IP相等,那么经过Hash(IP)之后的哈希值是相同的,将此哈希值取模(如模1000),必定仍然相等。
- 那到底什么是hash映射呢? 简单来说,就是为了便于计算机在有限的内存中处理big数据,从而通过一种映射散列的方式让数据均匀分布在对应的内存位置(如大数据通过取余的方式映射成小树存放在内存中,或大文件映射成多个小文件),而这个映射散列方式便是通常所说的hash函数,设计的好的hash函数能让数据均匀分布而减少冲突。尽管数据映射到了另外一些不同的位置,但数据还是原来的数据,只是代替和表示这些原始数据的形式发生了变化而已。
寻找热门查询,300万个查询字符串中统计最热门的10个查询
原题: 搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来,每个查询串的长度为1-255字节。假设目前有一千万个记录(这些查询串的重复度比较高,虽然总数是1千万,但如果除去重复后,不超过3百万个。一个查询串的重复度越高,说明查询它的用户越多,也就是越热门),请你统计最热门的10个查询串,要求使用的内存不能超过1G。
解答: 由上面第1题,知道,数据大则划为小的,如如一亿个Ip求Top 10,可先%1000将ip分到1000个小文件中去,并保证一种ip只出现在一个文件中,再对每个小文件中的ip进行hashmap计数统计并按数量排序,最后归并或者最小堆依次处理每个小文件的top10以得到最后的结。
但如果数据规模比较小,能一次性装入内存呢?比如这第2题,虽然有一千万个Query,但是由于重复度比较高,因此事实上只有300万的Query,每个Query255Byte,因此可以考虑把他们都放进内存中去(300万个字符串假设没有重复,都是最大长度,那么最多占用内存3M*1K/4=0.75G。所以可以将所有字符串都存放在内存中进行处理),而现在只是需要一个合适的数据结构,在这里,HashTable绝对是优先的选择。
所以放弃分而治之/hash映射的步骤,直接上hash统计,然后排序。So,针对此类典型的TOP K问题,采取的对策往往是: hashmap + 堆。如下所示:
hash_map统计: 先对这批海量数据预处理。具体方法是: 维护一个Key为Query字串,Value为该Query出现次数的HashTable,即hash_map(Query,Value),每次读取一个Query,如果该字串不在Table中,那么加入该字串,并且将Value值设为1;如果该字串在Table中,那么将该字串的计数加一即可。最终在O(N)的时间复杂度内用Hash表完成了统计; 堆排序: 第二步、借助堆这个数据结构,找出Top K,时间复杂度为N‘logK。即借助堆结构,可以在log量级的时间内查找和调整/移动。因此,维护一个K(该题目中是10)大小的小根堆,然后遍历300万的Query,分别和根元素进行对比。所以,最终的时间复杂度是: O(N) + N' * O(logK),(N为1000万,N’为300万)。
别忘了这篇文章中所述的堆排序思路: “维护k个元素的最小堆,即用容量为k的最小堆存储最先遍历到的k个数,并假设它们即是最大的k个数,建堆费时O(k),并调整堆(费时O(logk))后,有k1>k2>...kmin(kmin设为小顶堆中最小元素)。继续遍历数列,每次遍历一个元素x,与堆顶元素比较,若x>kmin,则更新堆(x入堆,用时logk),否则不更新堆。这样下来,总费时O(k*logk+(n-k)logk)=O(nlogk)。此方法得益于在堆中,查找等各项操作时间复杂度均为logk。”--第三章续、Top K算法问题的实现。 当然,你也可以采用trie树,关键字域存该查询串出现的次数,没有出现为0。最后用10个元素的最小推来对出现频率进行排序。
有一个1G大小的一个文件,里面每一行是一个词,词的大小不超过16字节,内存限制大小是1M。返回频数最高的100个词。
分而治之/hash映射: 顺序读文件中,对于每个词x,取hash(x)%5000,然后按照该值存到5000个小文件(记为x0,x1,...x4999)中。这样每个文件大概是200k左右。如果其中的有的文件超过了1M大小,还可以按照类似的方法继续往下分,直到分解得到的小文件的大小都不超过1M。hash_map统计: 对每个小文件,采用trie树/hash_map等统计每个文件中出现的词以及相应的频率。堆/归并排序: 取出出现频率最大的100个词(可以用含100个结点的最小堆)后,再把100个词及相应的频率存入文件,这样又得到了5000个文件。最后就是把这5000个文件进行归并(类似于归并排序)的过程了。
海量数据分布在100台电脑中,想个办法高效统计出这批数据的TOP10。
如果每个数据元素只出现一次,而且只出现在某一台机器中,那么可以采取以下步骤统计出现次数TOP10的数据元素:
堆排序: 在每台电脑上求出TOP10,可以采用包含10个元素的堆完成(TOP10小,用最大堆,TOP10大,用最小堆,比如求TOP10大,首先取前10个元素调整成最小堆,如果发现,然后扫描后面的数据,并与堆顶元素比较,如果比堆顶元素大,那么用该元素替换堆顶,然后再调整为最小堆。最后堆中的元素就是TOP10大)。 求出每台电脑上的TOP10后,然后把这100台电脑上的TOP10组合起来,共1000个数据,再利用上面类似的方法求出TOP10就可以了。
但如果同一个元素重复出现在不同的电脑中呢,如下例子所述, 这个时候,你可以有两种方法:
- 遍历一遍所有数据,重新hash取摸,如此使得同一个元素只出现在单独的一台电脑中,然后采用上面所说的方法,统计每台电脑中各个元素的出现次数找出TOP10,继而组合100台电脑上的TOP10,找出最终的TOP10。
- 或者,暴力求解: 直接统计统计每台电脑中各个元素的出现次数,然后把同一个元素在不同机器中的出现次数相加,最终从所有数据中找出TOP10。
有10个文件,每个文件1G,每个文件的每一行存放的都是用户的query,每个文件的query都可能重复。要求你按照query的频度排序。
方案1:
hash映射: 顺序读取10个文件,按照hash(query)%10的结果将query写入到另外10个文件(记为a0,a1,..a9)中。这样新生成的文件每个的大小大约也1G(假设hash函数是随机的)。hash_map统计: 找一台内存在2G左右的机器,依次对用hash_map(query, query_count)来统计每个query出现的次数。注: hash_map(query,query_count)是用来统计每个query的出现次数,不是存储他们的值,出现一次,则count+1。 堆/快速/归并排序: 利用快速/堆/归并排序按照出现次数进行排序,将排序好的query和对应的query_cout输出到文件中,这样得到了10个排好序的文件(记为)。最后,对这10个文件进行归并排序(内排序与外排序相结合)。根据此方案1,这里有一份实现: https://github.com/ooooola/sortquery/blob/master/querysort.py。
方案2: 一般query的总量是有限的,只是重复的次数比较多而已,可能对于所有的query,一次性就可以加入到内存了。这样,就可以采用trie树/hash_map等直接来统计每个query出现的次数,然后按出现次数做快速/堆/归并排序就可以了。
方案3: 与方案1类似,但在做完hash,分成多个文件后,可以交给多个文件来处理,采用分布式的架构来处理(比如MapReduce),最后再进行合并。
给定a、b两个文件,各存放50亿个url,每个url各占64字节,内存限制是4G,让你找出a、b文件共同的url?
可以估计每个文件安的大小为5G×64=320G,远远大于内存限制的4G。所以不可能将其完全加载到内存中处理。考虑采取分而治之的方法。
分而治之/hash映射: 遍历文件a,对每个url求取,然后根据所取得的值将url分别存储到1000个小文件(记为,这里漏写个了a1)中。这样每个小文件的大约为300M。遍历文件b,采取和a相同的方式将url分别存储到1000小文件中(记为)。这样处理后,所有可能相同的url都在对应的小文件()中,不对应的小文件不可能有相同的url。然后只要求出1000对小文件中相同的url即可。
hash_set统计: 求每对小文件中相同的url时,可以把其中一个小文件的url存储到hash_set中。然后遍历另一个小文件的每个url,看其是否在刚才构建的hash_set中,如果是,那么就是共同的url,存到文件里面就可以了。
怎么在海量数据中找出重复次数最多的一个?
方案: 先做hash,然后求模映射为小文件,求出每个小文件中重复次数最多的一个,并记录重复次数。然后找出上一步求出的数据中重复次数最多的一个就是所求(具体参考前面的题)。
上千万或上亿数据(有重复),统计其中出现次数最多的前N个数据。
方案: 上千万或上亿的数据,现在的机器的内存应该能存下。所以考虑采用hash_map/搜索二叉树/红黑树等来进行统计次数。然后利用堆取出前N个出现次数最多的数据。
一个文本文件,大约有一万行,每行一个词,要求统计出其中最频繁出现的前10个词,请给出思想,给出时间复杂度分析。
方案1: 如果文件比较大,无法一次性读入内存,可以采用hash取模的方法,将大文件分解为多个小文件,对于单个小文件利用hash_map统计出每个小文件中10个最常出现的词,然后再进行归并处理,找出最终的10个最常出现的词。
方案2: 通过hash取模将大文件分解为多个小文件后,除了可以用hash_map统计出每个小文件中10个最常出现的词,也可以用trie树统计每个词出现的次数,时间复杂度是O(nle)(le表示单词的平准长度),最终同样找出出现最频繁的前10个词(可用堆来实现),时间复杂度是O(nlg10)。
一个文本文件,找出前10个经常出现的词,但这次文件比较长,说是上亿行或十亿行,总之无法一次读入内存,问最优解。
方案1: 首先根据用hash并求模,将文件分解为多个小文件,对于单个文件利用上题的方法求出每个文件件中10个最常出现的词。然后再进行归并处理,找出最终的10个最常出现的词。
100w个数中找出最大的100个数。
方案1: 采用局部淘汰法。选取前100个元素,并排序,记为序列L。然后一次扫描剩余的元素x,与排好序的100个元素中最小的元素比,如果比这个最小的要大,那么把这个最小的元素删除,并把x利用插入排序的思想,插入到序列L中。依次循环,知道扫描了所有的元素。复杂度为O(100w*100)。
方案2: 采用快速排序的思想,每次分割之后只考虑比轴大的一部分,知道比轴大的一部分在比100多的时候,采用传统排序算法排序,取前100个。复杂度为O(100w*100)。
方案3: 在前面的题中,已经提到了,用一个含100个元素的最小堆完成。复杂度为O(100w*lg100)。
Bitmap & Bloom Filter
分布式算法
一致性Hash算法
Paxos算法
Raft算法
ZAB算法
Snowflake算法
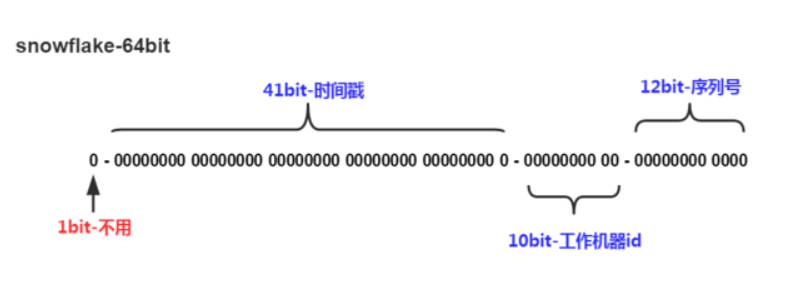
Snowflake,雪花算法是由Twitter开源的分布式ID生成算法,以划分命名空间的方式将 64-bit位分割成多个部分,每个部分代表不同的含义。而 Java中64bit的整数是Long类型,所以在 Java 中 SnowFlake 算法生成的 ID 就是 long 来存储的。
- 第1位占用1bit,其值始终是0,可看做是符号位不使用。
- 第2位开始的41位是时间戳,41-bit位可表示2^41个数,每个数代表毫秒,那么雪花算法可用的时间年限是
(1L<<41)/(1000L360024*365)=69 年的时间。 - 中间的10-bit位可表示机器数,即2^10 = 1024台机器,但是一般情况下不会部署这么台机器。如果对IDC(互联网数据中心)有需求,还可以将 10-bit 分 5-bit 给 IDC,分5-bit给工作机器。这样就可以表示32个IDC,每个IDC下可以有32台机器,具体的划分可以根据自身需求定义。
- 最后12-bit位是自增序列,可表示2^12 = 4096个数。
这样的划分之后相当于在一毫秒一个数据中心的一台机器上可产生4096个有序的不重复的ID。但是 IDC 和机器数肯定不止一个,所以毫秒内能生成的有序ID数是翻倍的。